During the derivation of the standard form equation from the geometric definition, we showed that the equation of an ellipse at the origin is:
To show that an ellipse is a stretched circle, we start with the equation of a circle:
If we want to stretch a shape in a graph by a factor of \(k\) on the \(x\)-axis, then we can achieve this by dividing the \(x\) variable by \(k\). For example, the function shown below is \(f(x)\). If we want to stretch it by a factor of \(k\) in the \(x\)-axis, we divide \(x\) by \(k\):
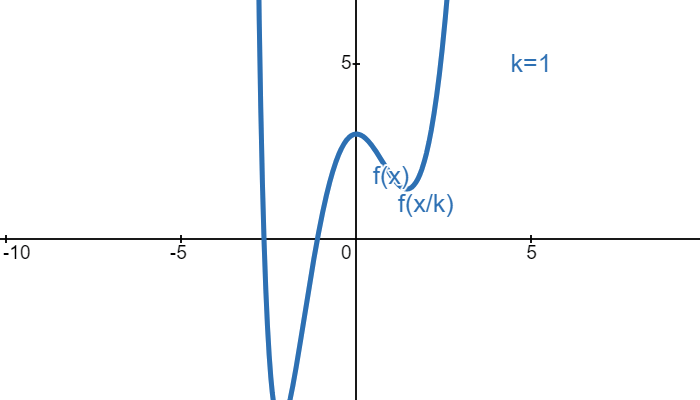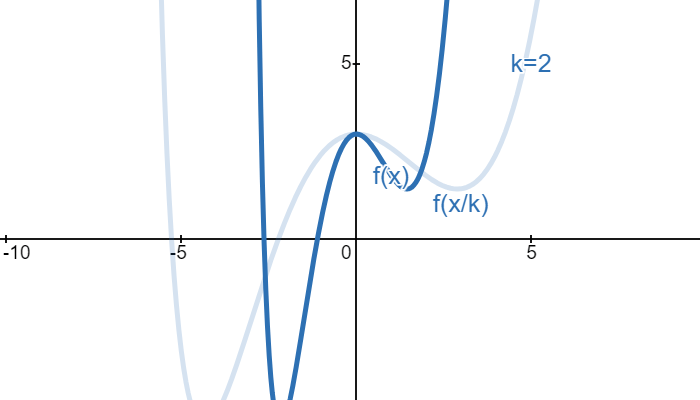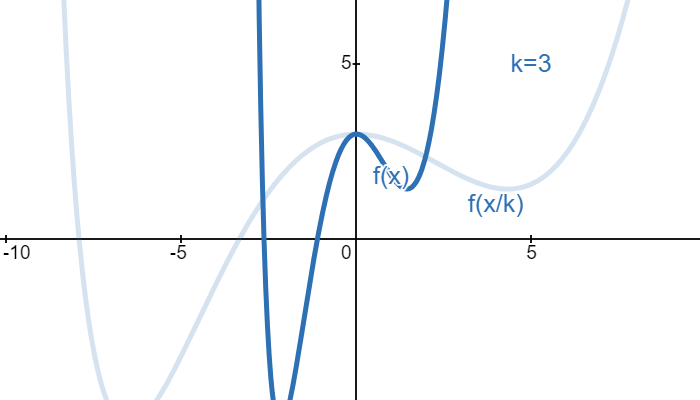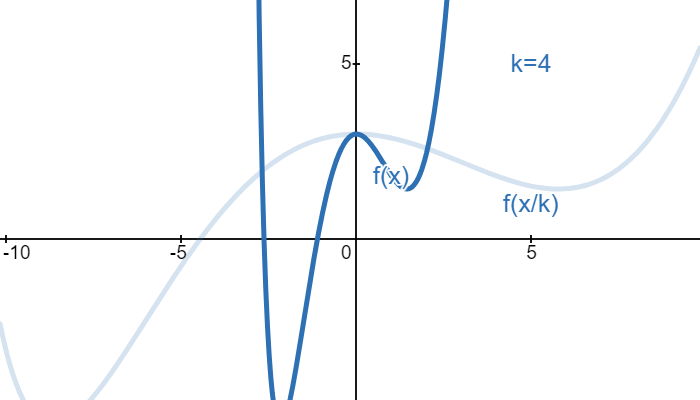
Consider a circle with radius \(r\). This circle would intersect the \(x\)-axis at \(x=r\) and \(x=-r\). Suppose we want to stretch or squish a circle on the \(x\)-axis so that the circle would then intersect the \(x\)-axis at \(x=a\) and \(x=-a\):
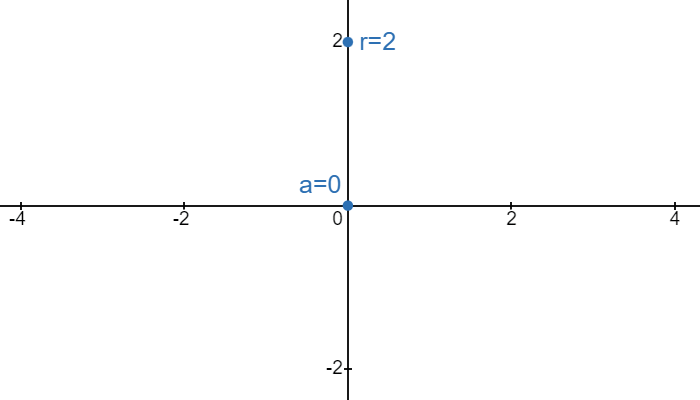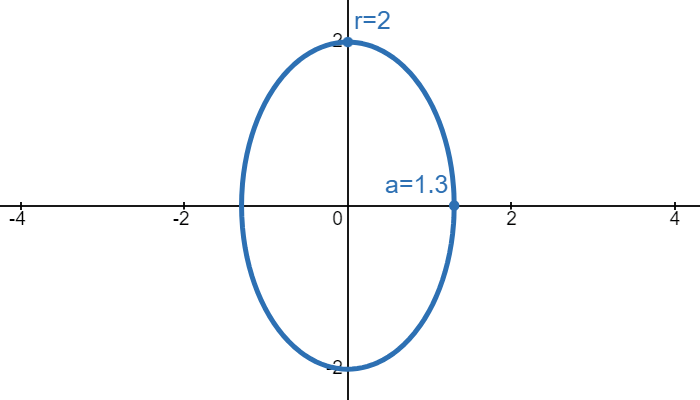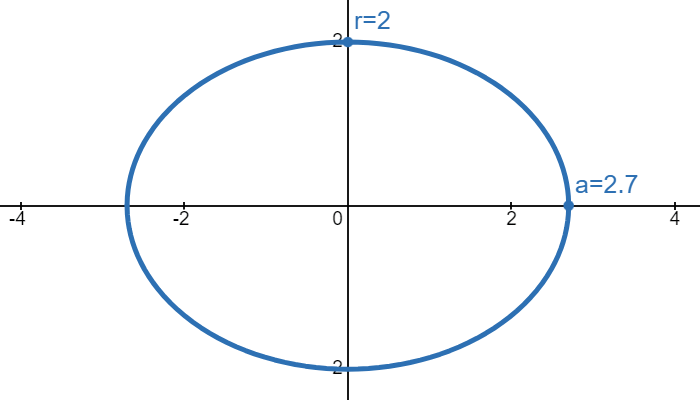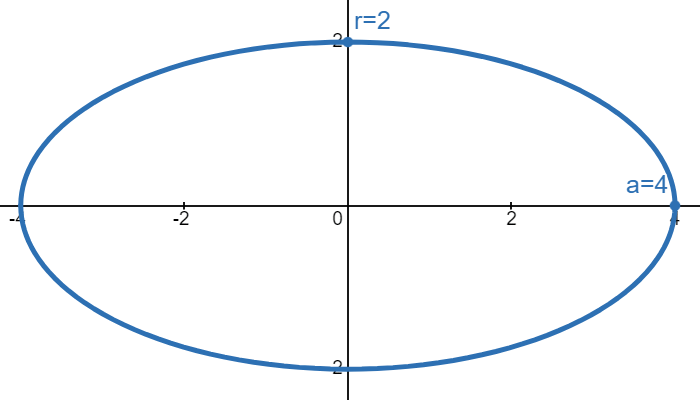
If we want stretch our circle so that the right end goes from \(x=r\) to \(x=a\), then we need to horizontally stretch the circle by a factor of \(\frac{a}{r}\). This means dividing the \(x\) in the circle equation by \(\frac{a}{r}\):
Rearranging:
This is the eqaution of an ellipse. If \(a > r\), then the major axis would be on the \(x\)-axis while the minor axis would be on the \(y\)-axis. If \(r > a\), then the major axis would be on the \(y\)-axis while the minor axis would be on the \(x\)-axis. If \(a=r\), then we would have a circle. Also, when learning about ellipses, you would often see the variable \(b\) being used in place of \(r\).