The definition of an ellipse is the set of all points for which the sum of their distances from two fixed points (the foci) is constant. Consider an ellipse where is centre is at the origin:
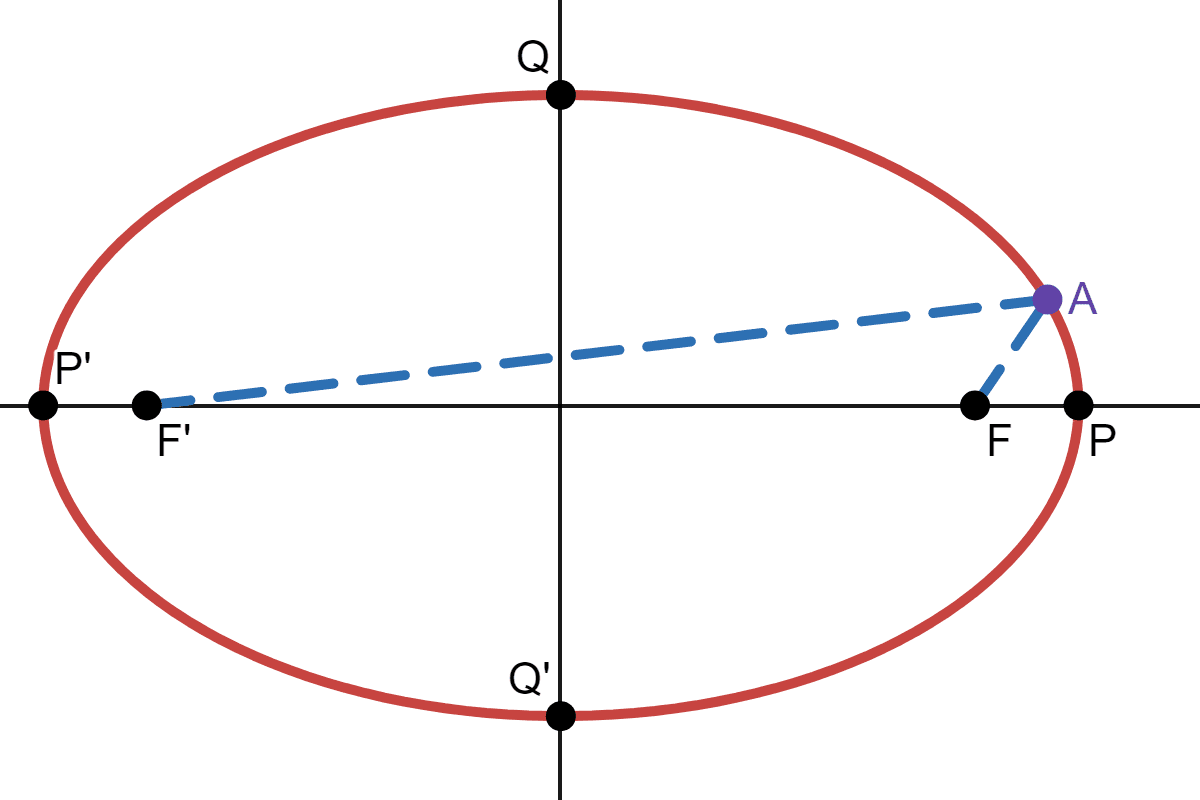
The points \(P\) and \(P'\) are located at the ends of the major axis of the ellipse, and have coordinates \((a,0)\) and \((-a,0)\), respectively. The major axis is always the longest distance across the ellipse, and can be horizontal or vertical. Thus, the length of the major axis in this ellipse is \(2a\). The points \(Q\) and \(Q'\) are located at the ends of the minor axis of the ellipse, and have coordinates \((0,b)\) and \((0,-b)\), respectively. The minor axis is the shortest distance across the ellipse. The minor axis is perpendicular to the major axis.
Let \(F=(c,0)\) and let \(A\) be a point of our choice. If \(A=P\) (i.e. \(y=0\) and \(x=a\)), then sum of the distances from \(A\) to both the foci is \((a+c) + (a-c)\) or \(2a\):
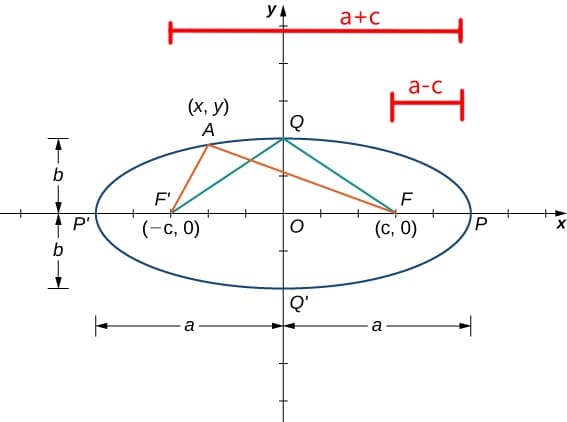
Since the sum of the distances from \(A\) to both the foci is constant, then for any \(A\), the sum of the distances would always be \(2a\). If \(A=Q\), then point \(A\) would be equidistant from the two foci, and so the distance from \(A\) to \(F\) would be \(a\). Using the Pythogorean theorem:
Consider the ellipse below:

Let \((x,y)\) be the coordinates of \(A\). The length of the smaller blue dashed line can be calculated using the Pythagorean theorem: \(\sqrt{(x-c)^2+y^2}\). Similarly, the larger blue dashed line is \(\sqrt{(x-(-c))^2+y^2}\) or \(\sqrt{(x+c)^2+y^2}\). Since their sum is \(2a\):
Squaring both sides:
Expanding:
Rearranging:
Expanding again:
Rearranging again:
Since \(a^2 = b^2 + c^2\):
Now we finally we a simple equation for our ellipse:
If the ellipse is shifted \(h\) units to the right and \(k\) units up: