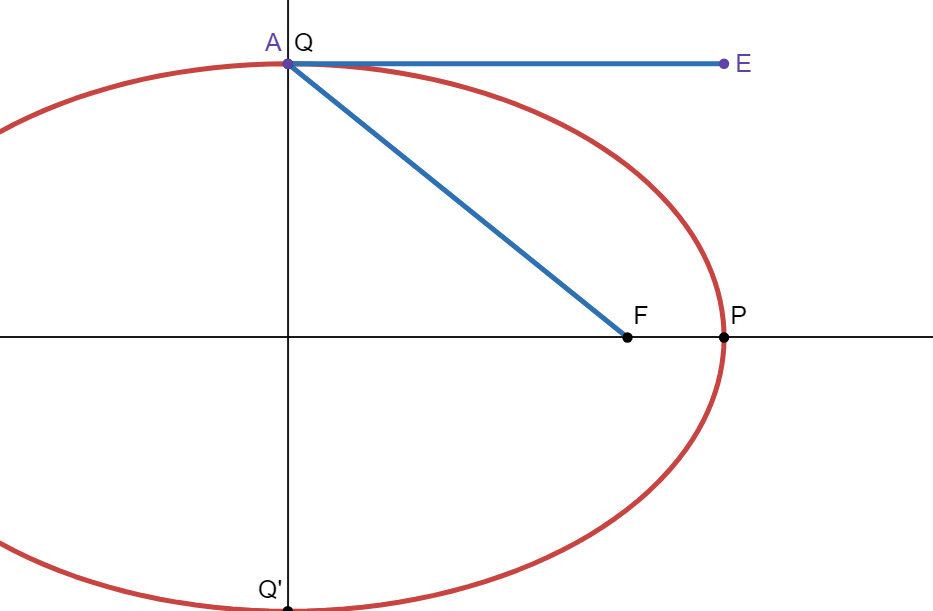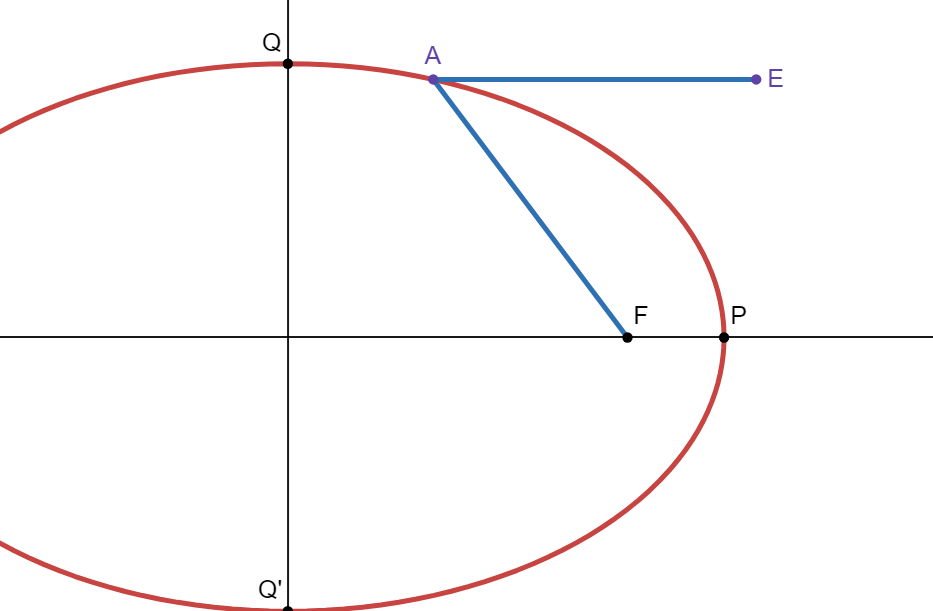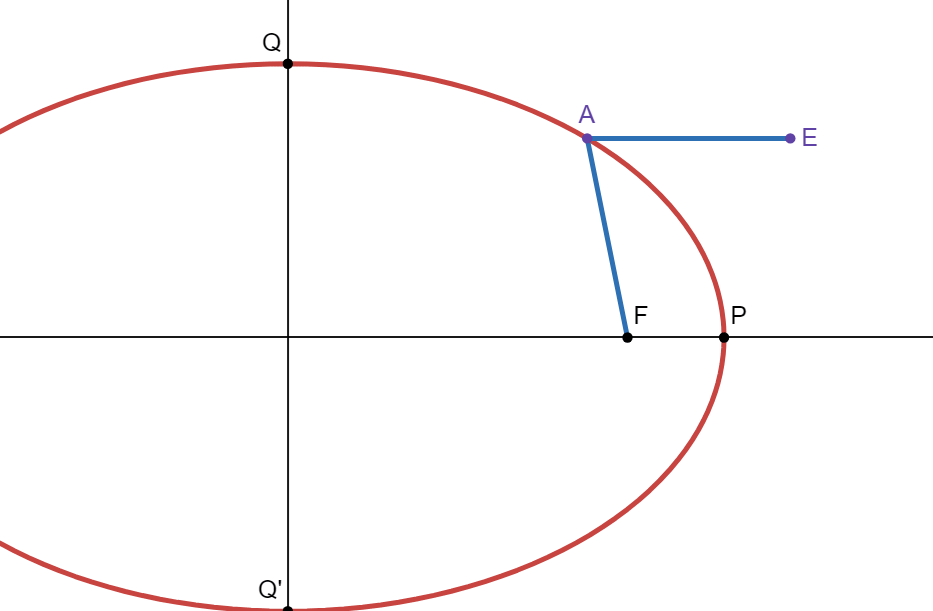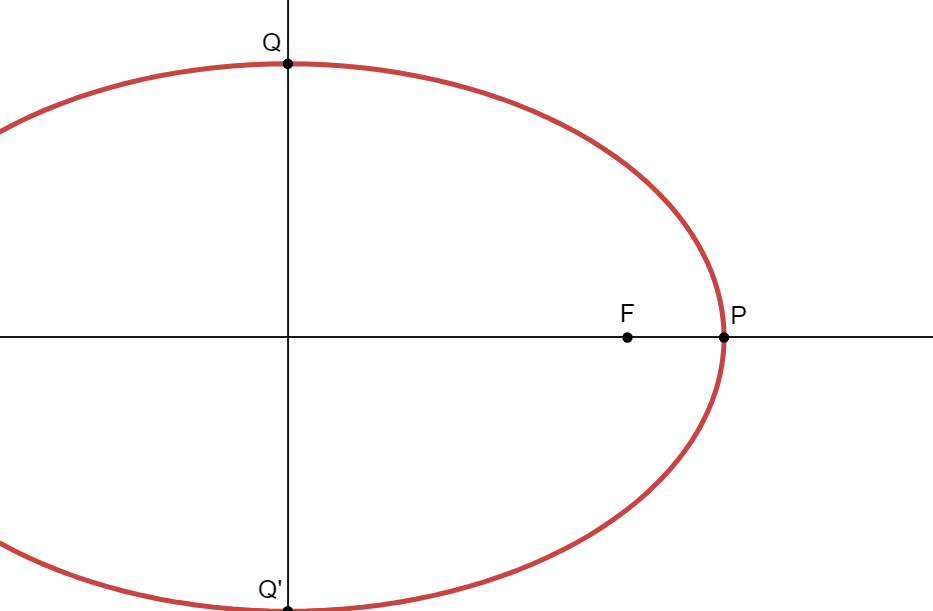
The definition of an ellipse is the set of all points for which the sum of their distances from two fixed points (the foci) is constant. Consider an ellipse where is centre is at the origin:
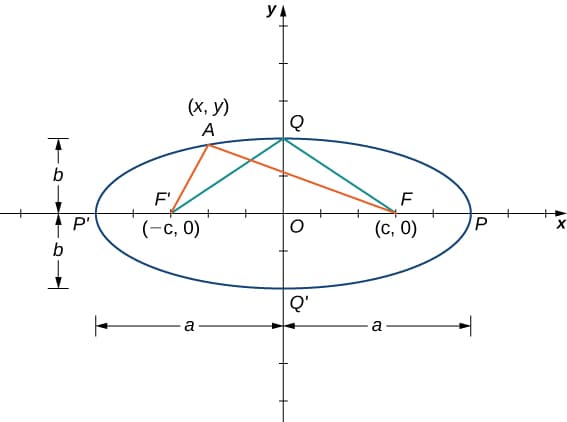
The points \(P\) and \(P'\) are located at the ends of the major axis of the ellipse, and have coordinates \((a,0)\) and \((-a,0)\), respectively. The length of the major axis in this ellipse is \(2a\). The points \(Q\) and \(Q'\) are located at the ends of the minor axis of the ellipse, and have coordinates \((0,b)\) and \((0,-b)\), respectively. Using these definitions, we can derive the standard form equation:
Choose a point \(A\) in the ellipse. Let \(d_A\) be the distance from \(A\) to one of the focus (we will only consider the right focus for now). Now image a horizontal line from \(A\) of length \(d_A\). Call the other end of this line \(E\):
We chose the length of the horizontal line such that \(\Vert FA \Vert = \Vert AE \Vert \). Now consider two points on the ellipse, one at \((0,b)\), and the other at \((a,0)\). We will call them \(X_1\) and \(X_2\) respectively:
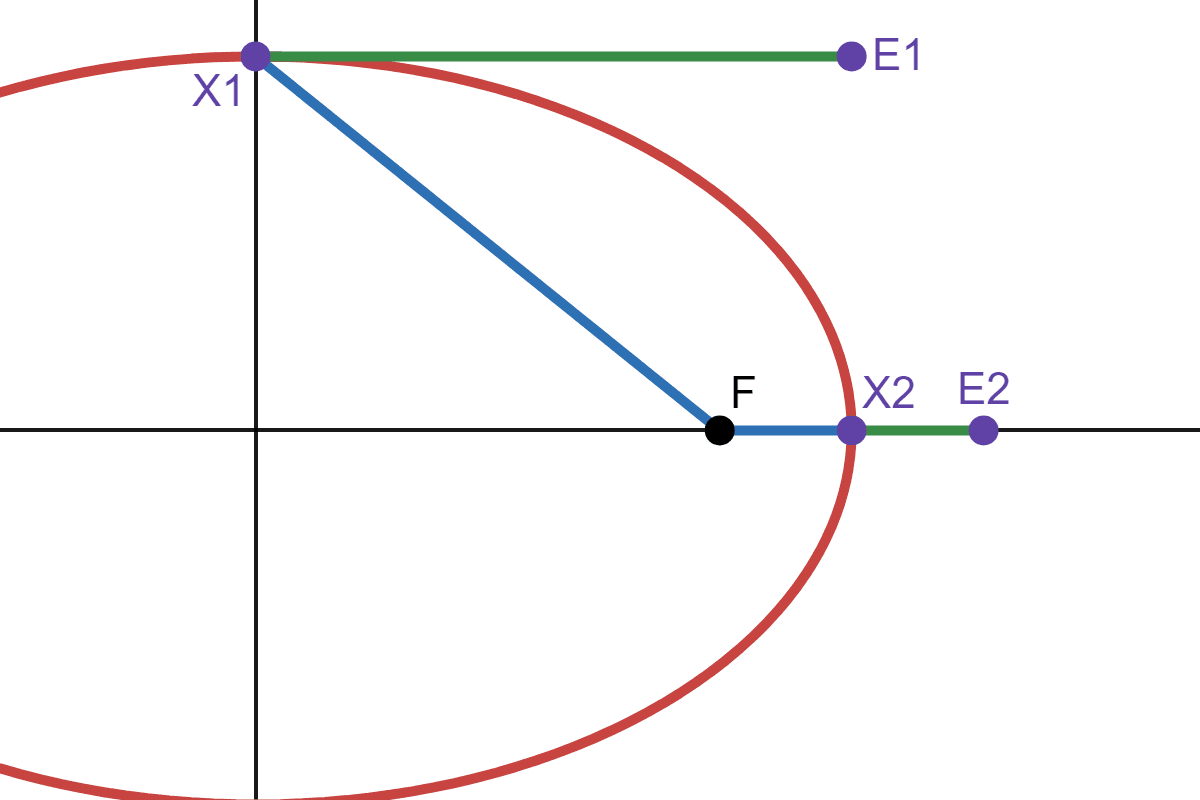
\(E_1\) and \(E_2\) are chosen such that \(\Vert F \ X_1 \Vert = \Vert X_1 \ E_1 \Vert \) and \(\Vert F \ X_2 \Vert = \Vert X_2 \ E_2 \Vert \). Choose a number \(k>0\), and let the lines from \(X_i\) to \(E_i\) be stretched or shrinked by a factor of \(k\). In other words \(\Vert X_i \ E_i \Vert = \Vert F \ X_i \Vert * k\).
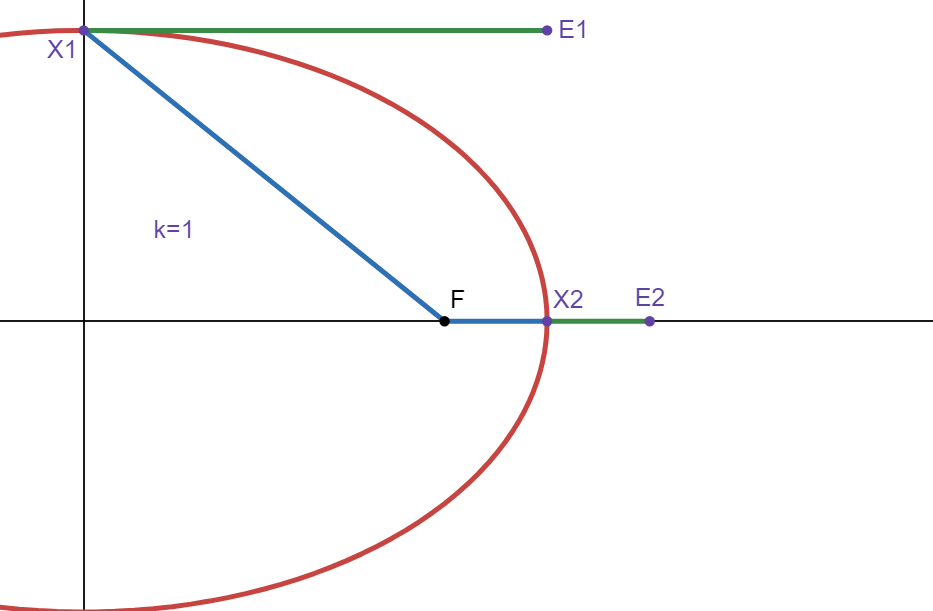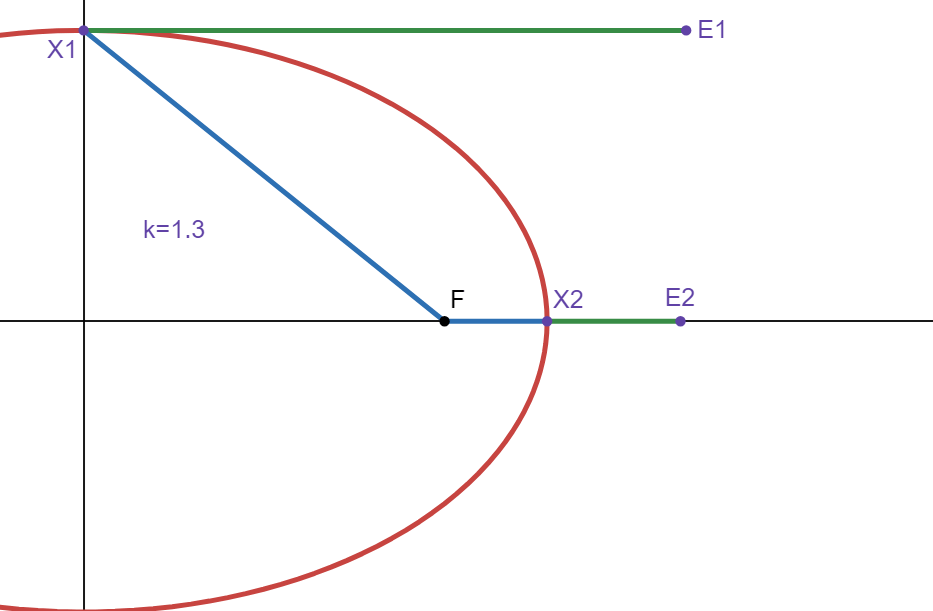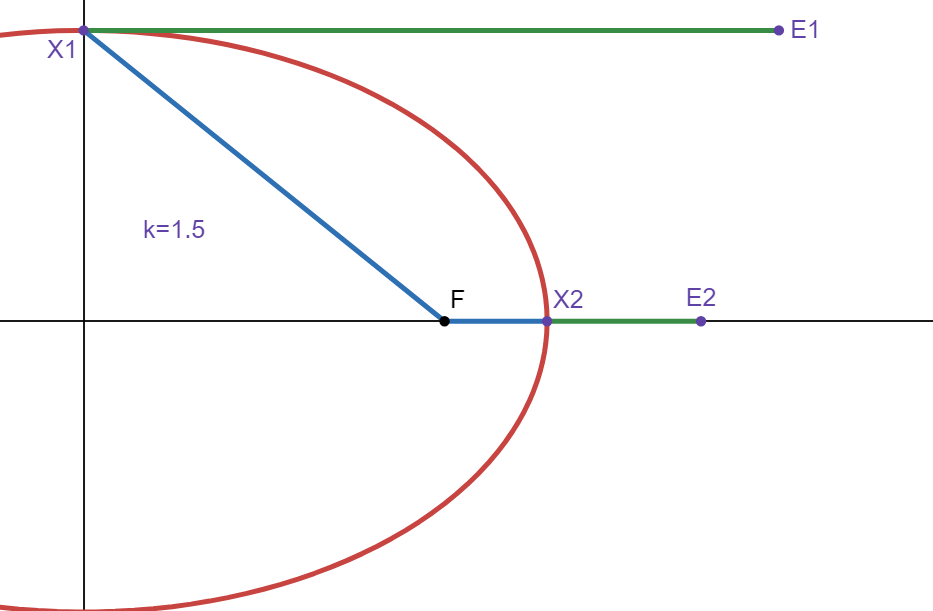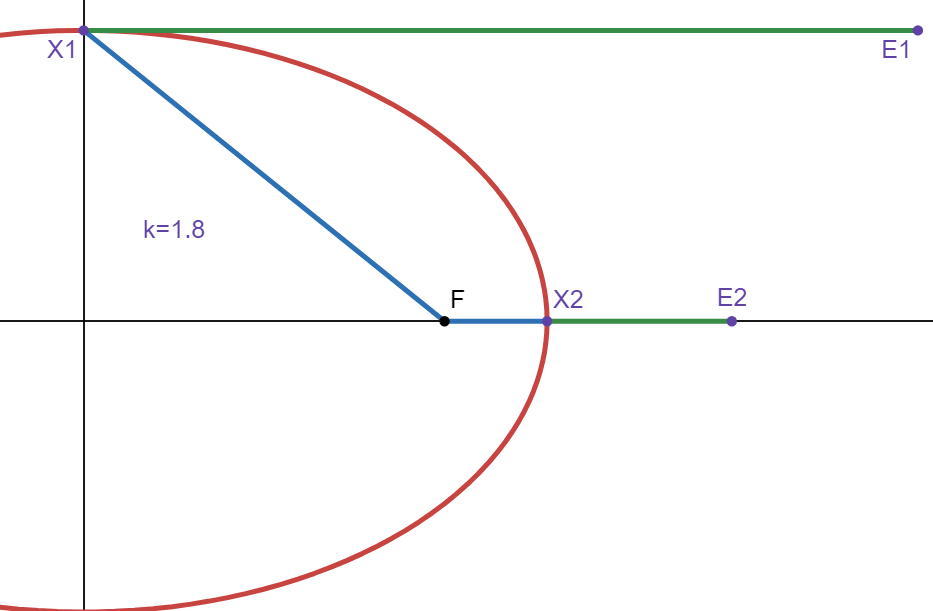
Let \(P_x\) be a function that gives only the \(x\) position of a point, so \(P_x(E_1) = ak\). Since \(\Vert P_x(X_2) = a \Vert \) and \(\Vert X_2 \ E_2 \Vert = \Vert F \ X_2 \Vert * k\), then:
Since \(P_x(E_1) = ak\) and \(P_x(E_2) = ak + (a-ck)\), then \(P_x(E_2) = P_x(E_1) + (a-ck)\). Let there be a number \(h>0\) such that \((a=ch)\), or \(a-ch=0\). Since \(P_x(E_2) = P_x(E_1) + (a-ck)\):
This means \(h\) is a unique value such that \(P_x(E_2) = P_x(E_1)\). If \(a=ch\), then \(h=\frac{a}{c}\). When \(k=h\), \(P_x(E_1) = a * \frac{a}{c}\). This means \(x=\frac{a^2}{c}\) is the line where \(E_1\) lies. Since \(E_2\) has the same \(x\) position at \(k=h\). Therefore, \(E_2\) also lies on the line \(x=\frac{a^2}{c}\):

Now choose a new random point \(A=(x_A,y_A)\) on the ellipse, and let there be a horizontal line going from \(A\) to some point \(E_A\). Is it true that when \(k=h\) and \(P_x(E_1)\) lies on \(x=\frac{a^2}{c}\), then \(P_x(E_A)\) would also lie on \(x=\frac{a^2}{c}\)? The length from \(A\) to \(F\) is \(\sqrt{(y_A)^2 + (x_A-c)^2}\):
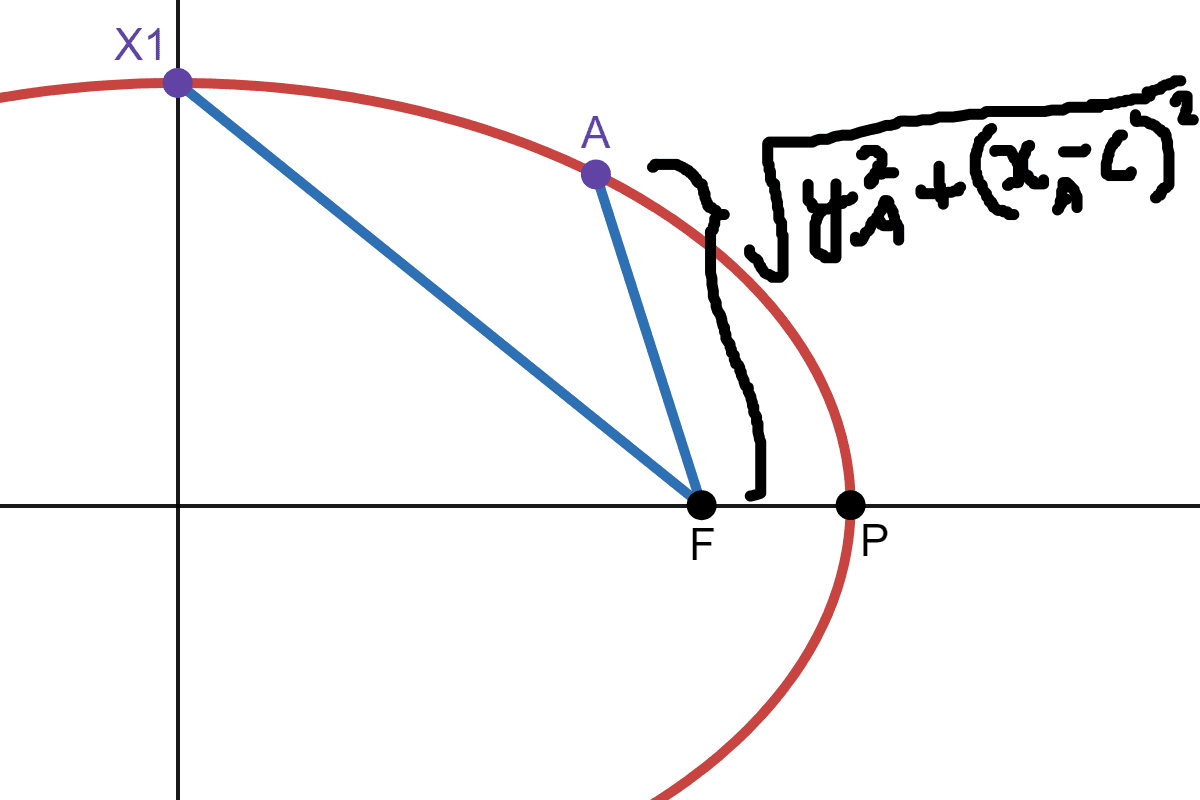
Let there be \(j > 0\), such that when \(k=j\), \(P_x (E_1) = P_x (E_A)\). This means:
Rearranging:
The equation for a point in an ellipse is:
Substituting for \(y_A\) in the previous equation:
The coefficients of \(x^2\) should be equal on both sides. The same should be true for \(x\), and for the terms without any \(x\):
Simplifying:
The second equation tells us that \(j = \frac{a}{c}\), which is the same value of \(k\) we got before with \(E_2\). This means when \(\Vert A \ E_A \Vert = \Vert A \ F \Vert * \frac{a}{c}\), then \(P_x(E_A) = P_x(E_1) = \frac{a^2}{c}\).
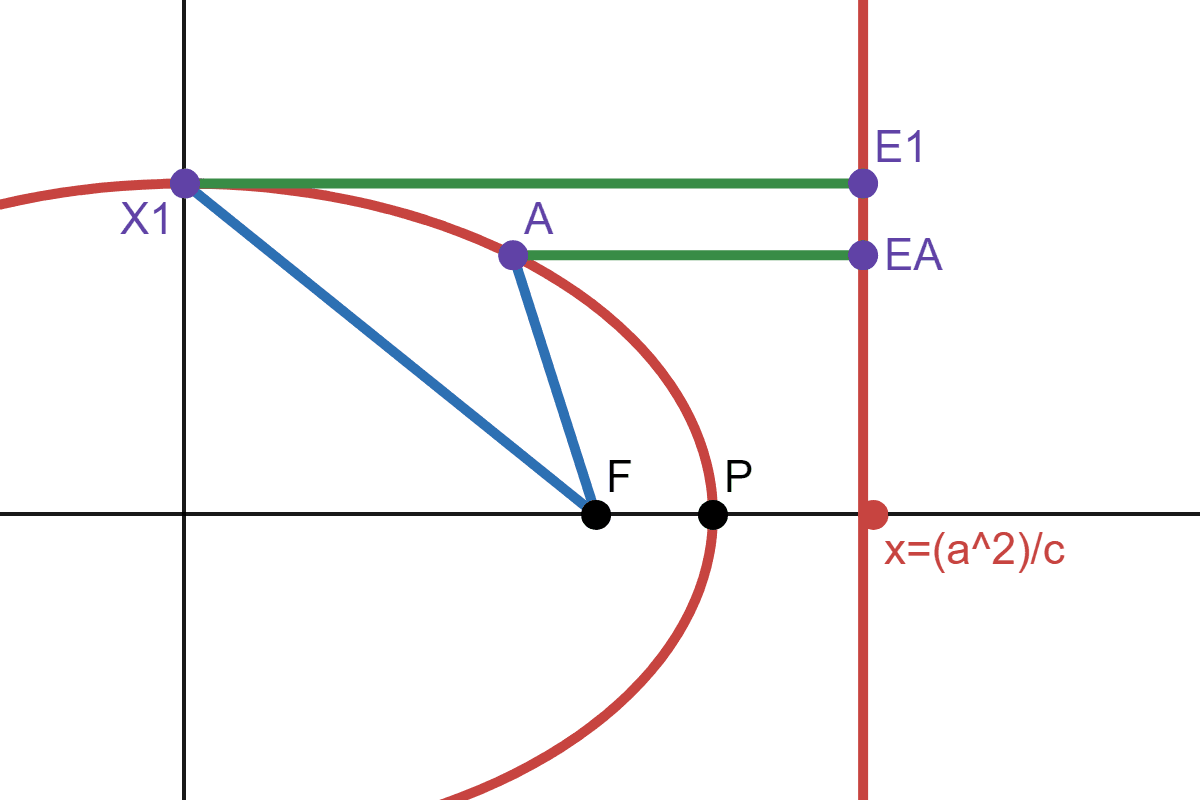
Thus, we have proven that for any point \(A\), the distance from point \(A\) to the line \(x=\frac{a^2}{c}\) divided by the distance from point \(A\) to the focus is always constant, and this constant ratio is \(\frac{a}{c}\). The line \(x=\frac{a^2}{c}\) is called the directrix. This is the focus-directrix definition of an ellipse.