Lets say [y = logbx], which means:
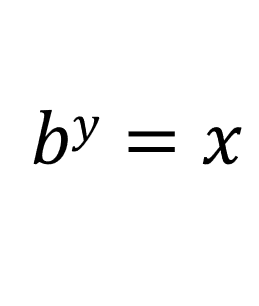
Now lets differentiate both sides with respect to x:
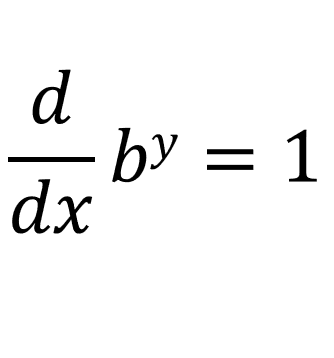
Instead of doing [[d/dx](by)], we can do this [[dy/dx] * [d/dy](by)]:
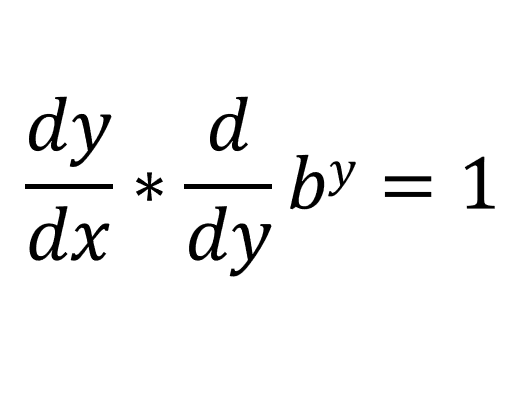
You should already know that [[d/dy](by) = (by * ln(b))] (if you don't, then click here):
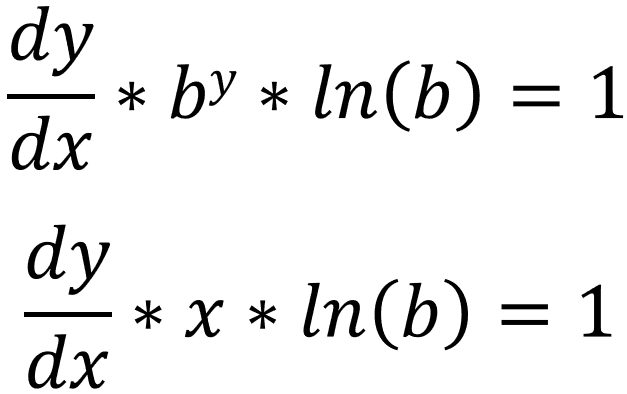
We can write this as:
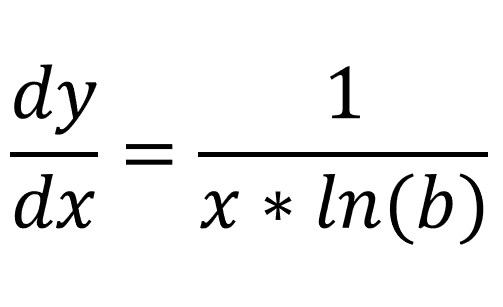
And that completes our proof.