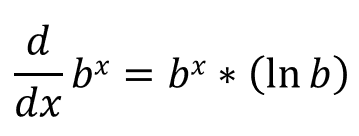For this proof, it must be clear to you that [d/dx](ex) = ex. Also, bx can be written as:
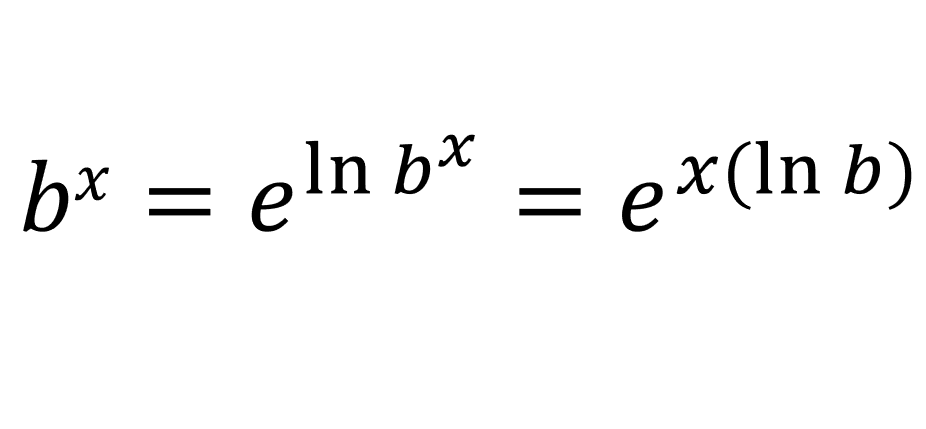
Now lets use the chain rule:
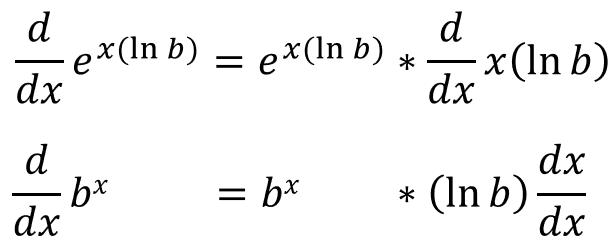
And that completes our proof.
Proof That [d/dx](b^x) = (b^x) * ln(b)
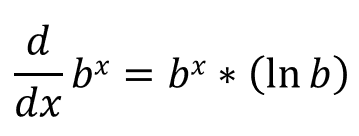
For this proof, it must be clear to you that [d/dx](ex) = ex. Also, bx can be written as:
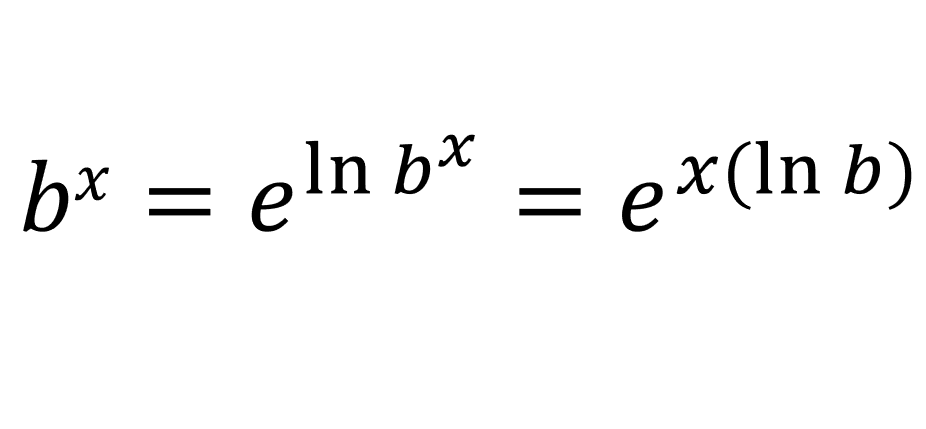
Now lets use the chain rule:
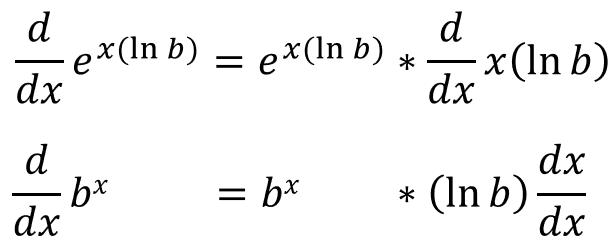
And that completes our proof.