Proof That (cos(x)-1)/x approaches 0 as x approaches 0

We want to prove that [lim_x->0 (cos(x)-1)/x = 0], which can be written as:

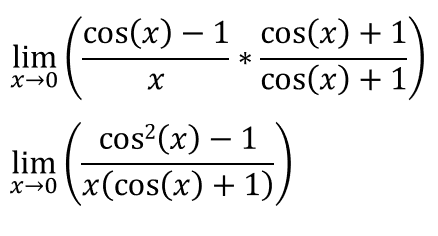
Since [cos²(x) + sin²(x) = 1], we can write:

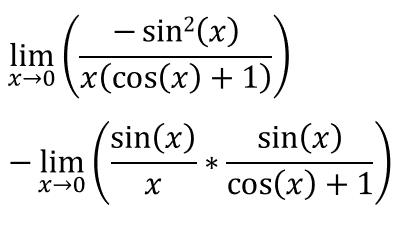
We can then use the product law:

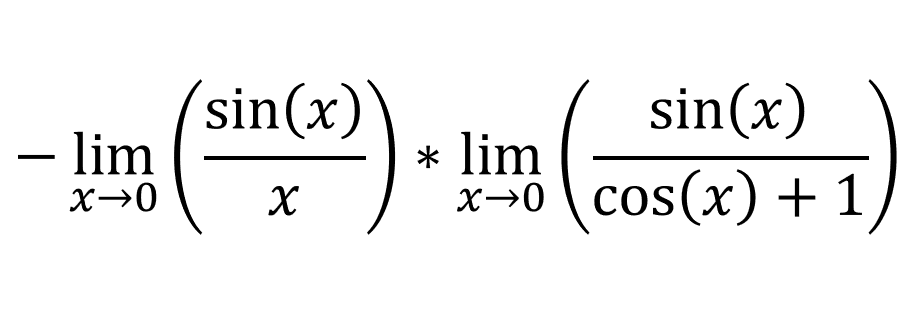
We know that [lim_x->0 sin(x)/x= 1], if you don't then click here. Evaluating the limits give us:

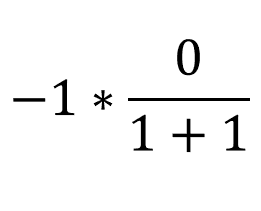
Which we know is equal to 0. Therefore [lim_x->0 (cos(x)-1)/x = 0].