Proof That sin(x)/x approaches 1 as x approaches 0

Suppose I have a circle with radius 1 and I want to find the area of the pink region bounded by the purple line and the x-axis :

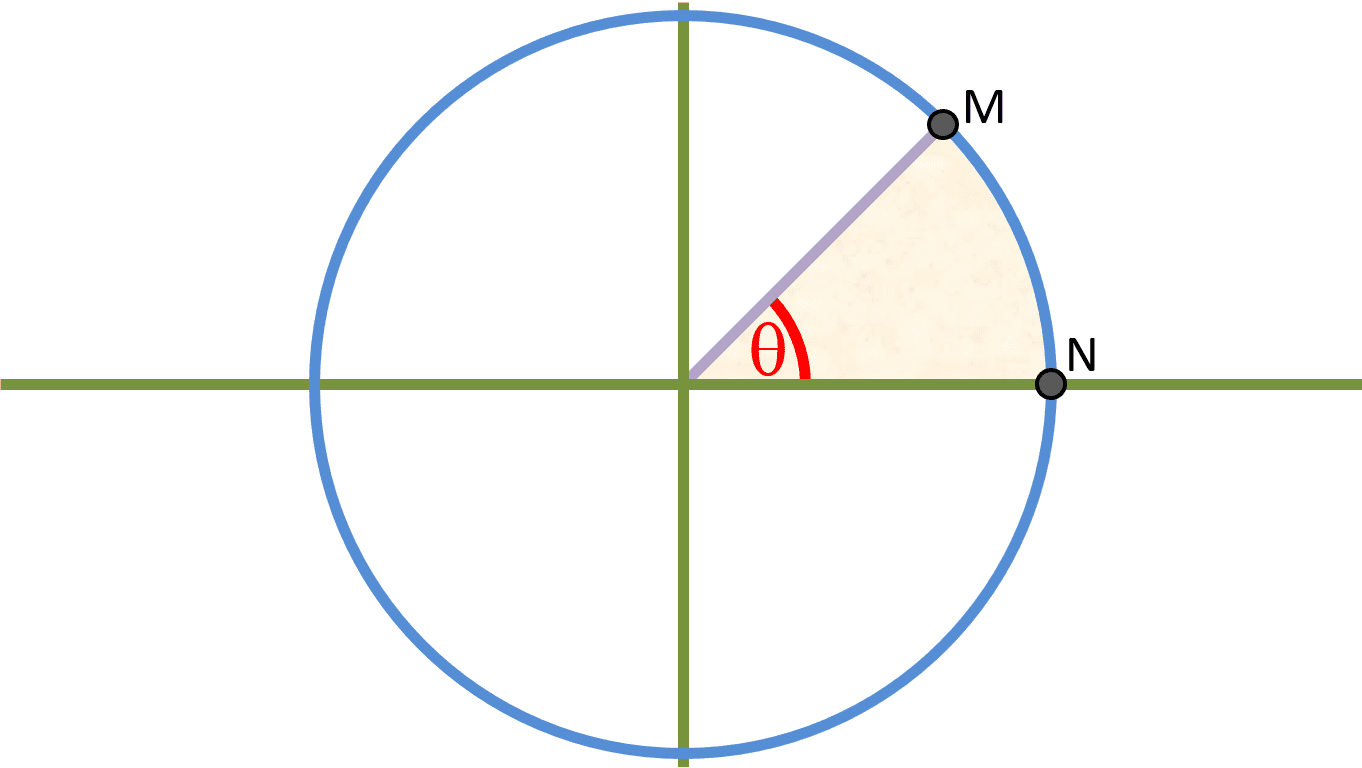
Let point M be the point where the purple line touches the circle and let point N be the point where the x-axis touches the circle. The formula for finding the area of a sector of a circle with raduis 1 is:

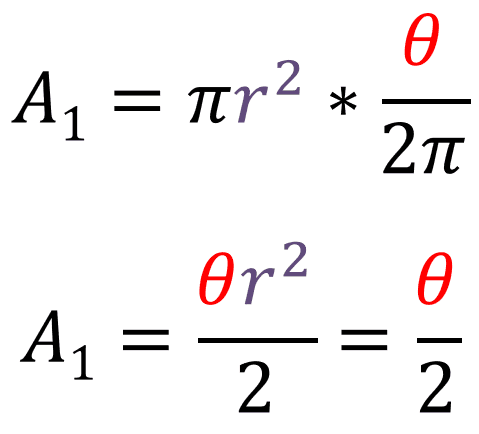
Now lets make a triangle by connecting points M and N:

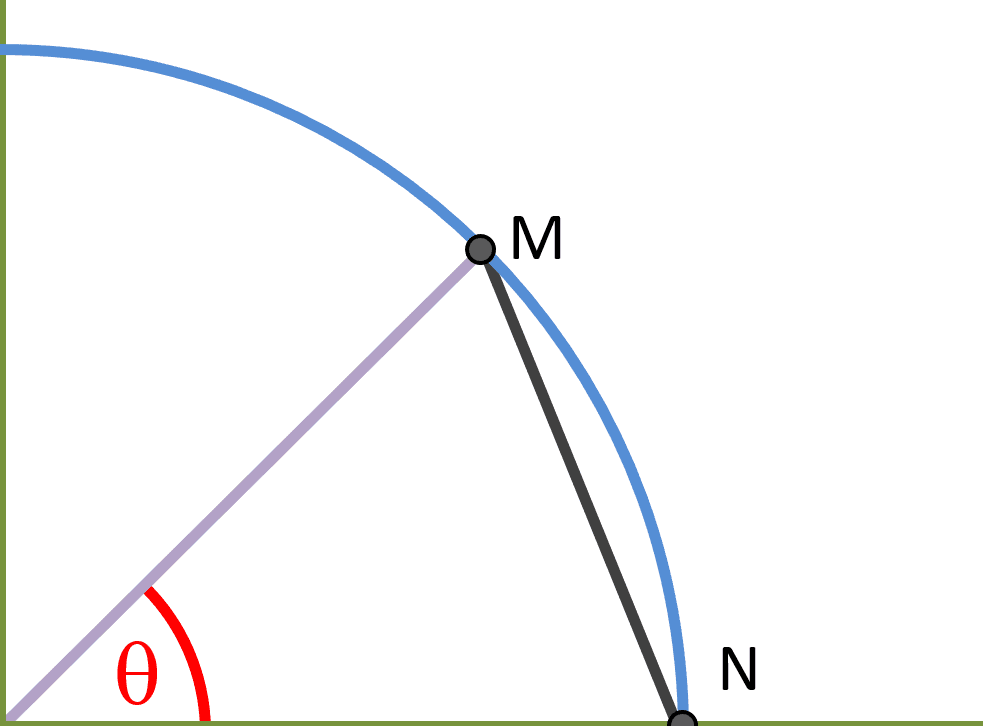
Since the height of this triangle is [sin(θ)] and the base is 1, then the area of the triangle is:

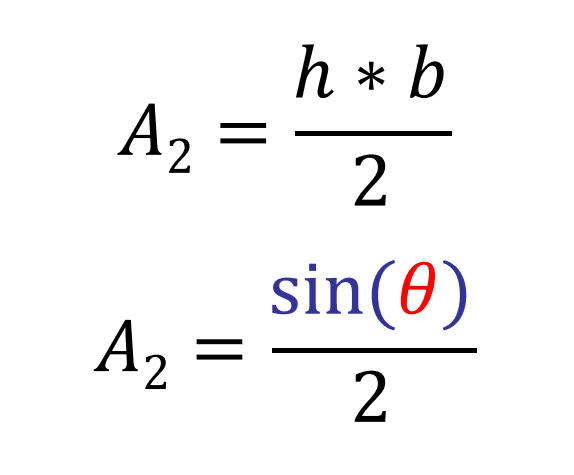
We know that A 2 \leq A 1 . Now lets create a smaller circle inside the main circle which has the radius of [cos(θ)]:

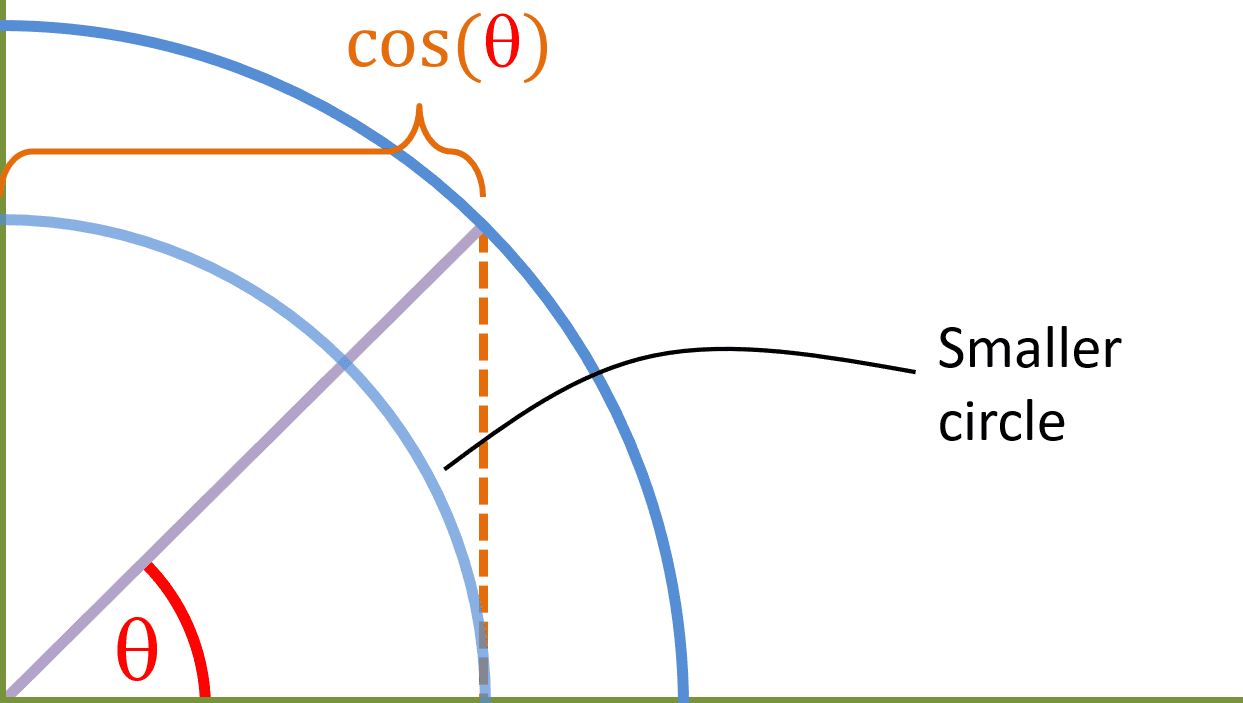
The area bounded by the purple line in the smaller circle and the x-axis has the following equation:

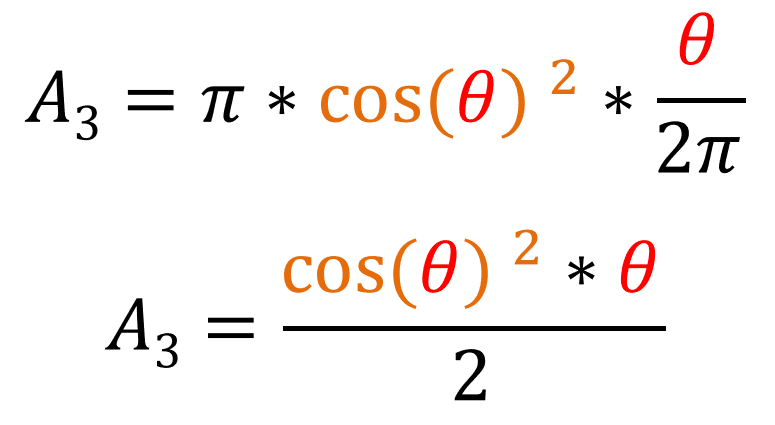
We know that A 3 \leq A 2 \leq A 1, which can be written as:

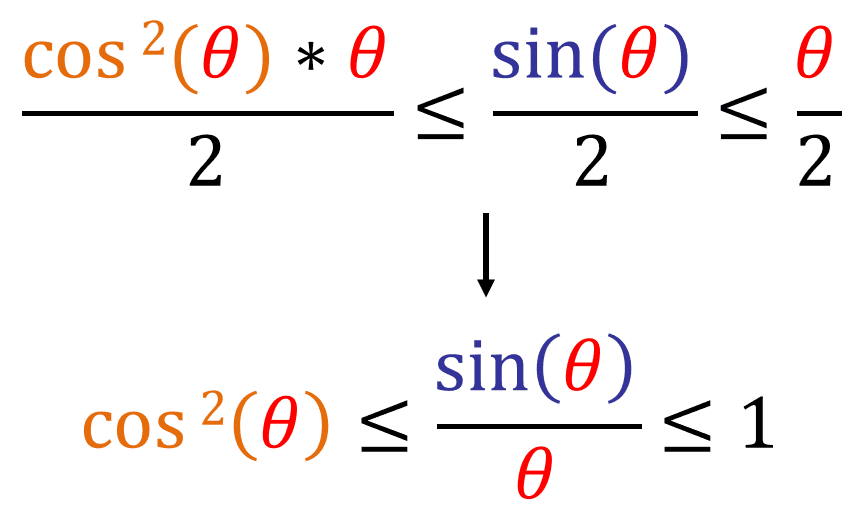
Now lets take the limit of all sides as x approaches 0:

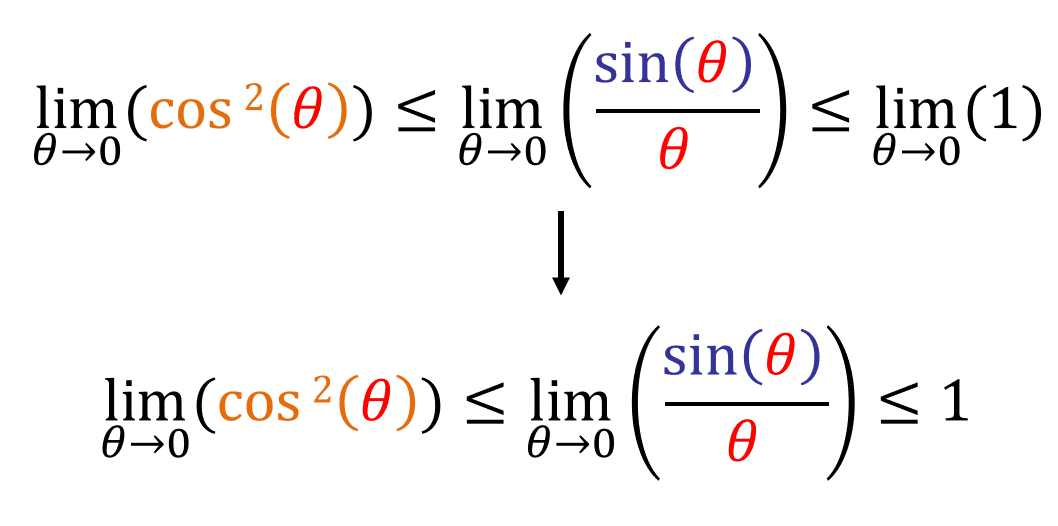
Since [lim θ->0 (cos(θ)) = 1], then, by the squeeze theorem, lim θ->0 (sin(θ) / θ) has to be 1. Keep in mind that this only works if θ is in radians.

\[ \lim_{\theta \to 0} \frac{ \color{#333399} \sin( {\color{red} \theta} )}{\color{red} \theta} = 1\]

To change an angle from radians to degrees, you multiply it by \(\frac{180}{\pi}\). Let \( \frac{180}{\pi} \theta = \alpha \), and let's say sin now uses degrees:

\[\begin{align} \lim_{\theta \to 0} \frac{ \color{#333399} \sin( {\color{black} \alpha} )}{\color{red} \theta} &= 1 \\ \lim_{\theta \to 0} \frac{\frac{180}{\pi} {\color{#333399} \sin( {\color{black} \alpha} )}}{ \frac{180}{\pi} {\color{red} \theta}} = \lim_{\theta \to 0} \frac{\frac{180}{\pi} {\color{#333399} \sin( {\color{black} \alpha} )}}{ \alpha } &= \left(\frac{180}{\pi} \right) \lim_{\theta \to 0} \frac{ {\color{#333399} \sin( {\color{black} \alpha} )}}{ \alpha } = 1 \end{align}\]

That means if you use degrees, then:

\[ \lim_{\theta \to 0} \frac{ {\color{#333399} \sin( {\color{black} \alpha} )}}{ \alpha } = \frac{\pi}{180} \]