Here is a circle with the radius of one:
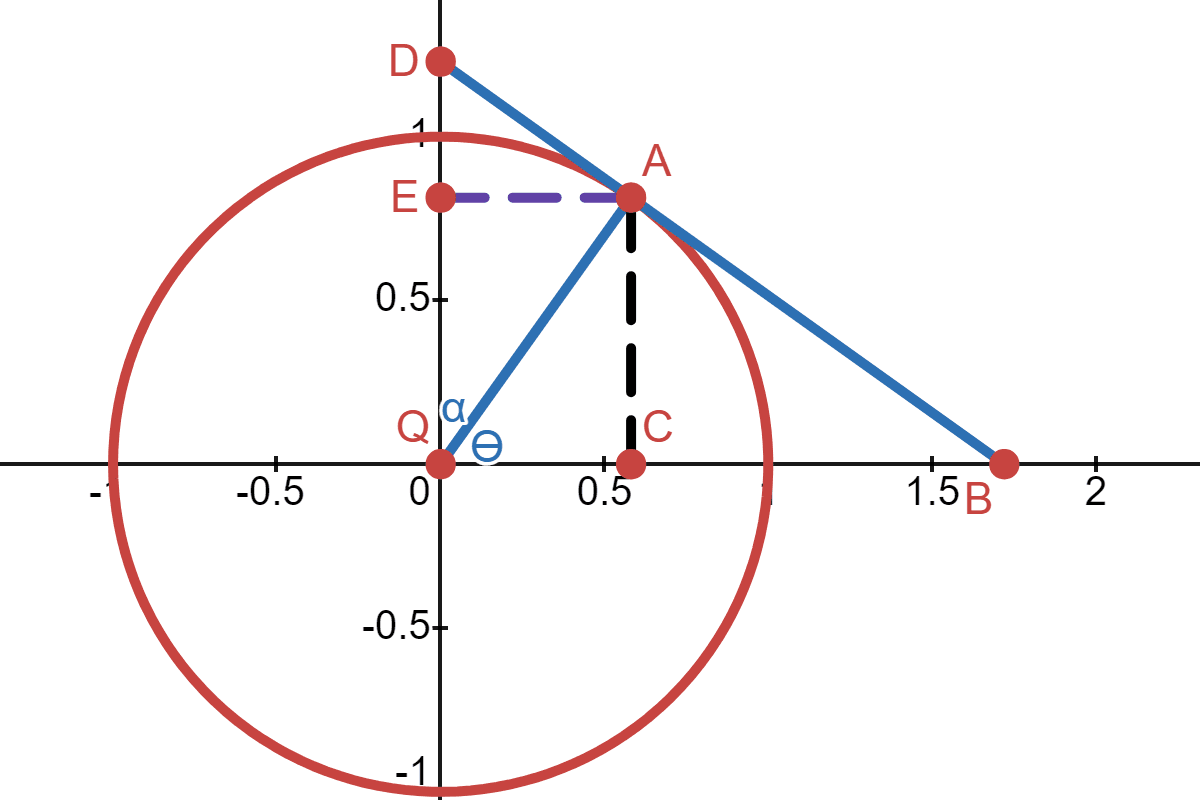
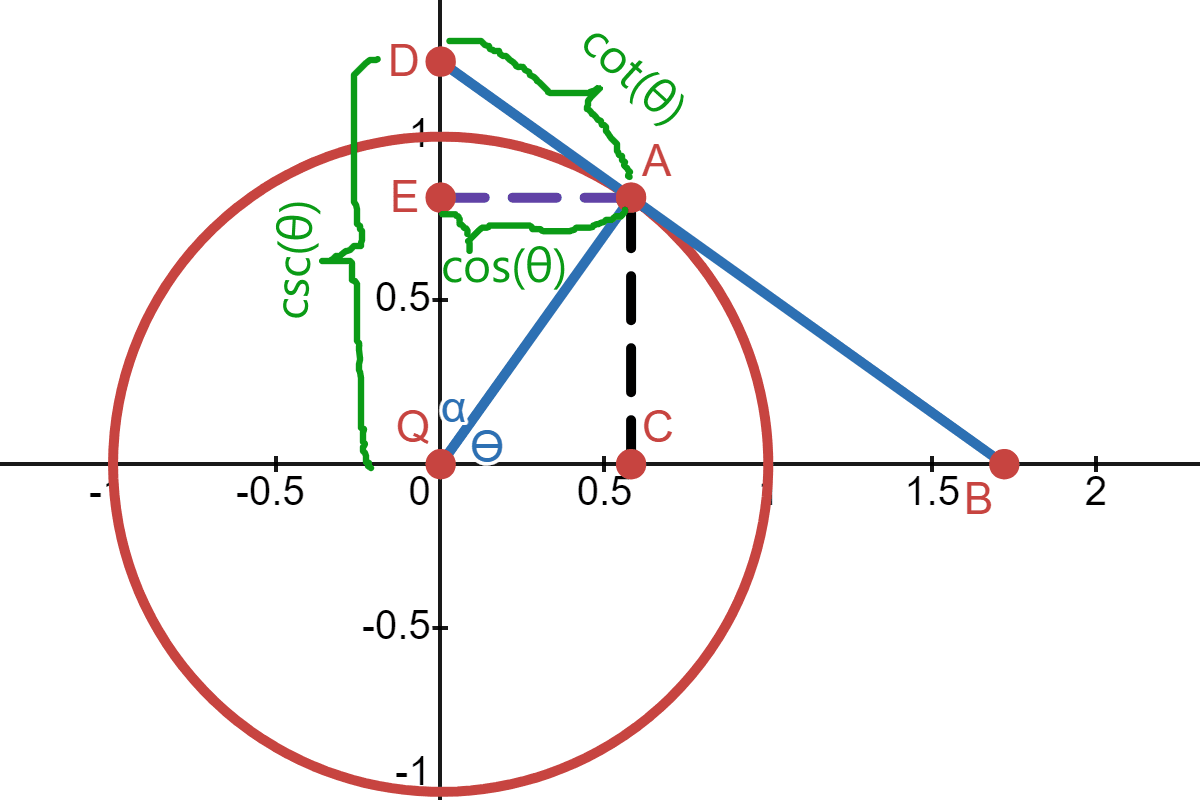
The angle \(\theta\) is the angle between the radius \(\overline{QA}\) and the x-axis. Also, \(\angle QCA\) and \(\angle QAB\) are both 90°.
In the triangle \(QCA\), the line \(\overline{AC}\) is the line opposite of \(\theta\), and the line \(\overline{QC}\) is the adjacent line. The function \(\operatorname{sine} (\theta)\) or \(\sin (\theta)\) is defined as the length of the opposite side \(\overline{AC}\) given that the hypotenuse is 1.
In the triangle \(QAB\), \(\overline{AB}\) is the opposite side, \(\overline{QA}\) is the adjacent side and \(\overline{QB}\) is the hypotenuse side. The function \(\operatorname{tangent} (\theta)\) or \(\tan (\theta)\) is defined as the length of the tangent line \(\overline{AB}\) (i.e. the opposite side) given that the adjacent is 1. Also, the function \(\operatorname{secant}(\theta)\) or \(\sec(\theta)\) is defined as the hypotenuse side \(\overline{QB}\), given that the adjacent side is 1.
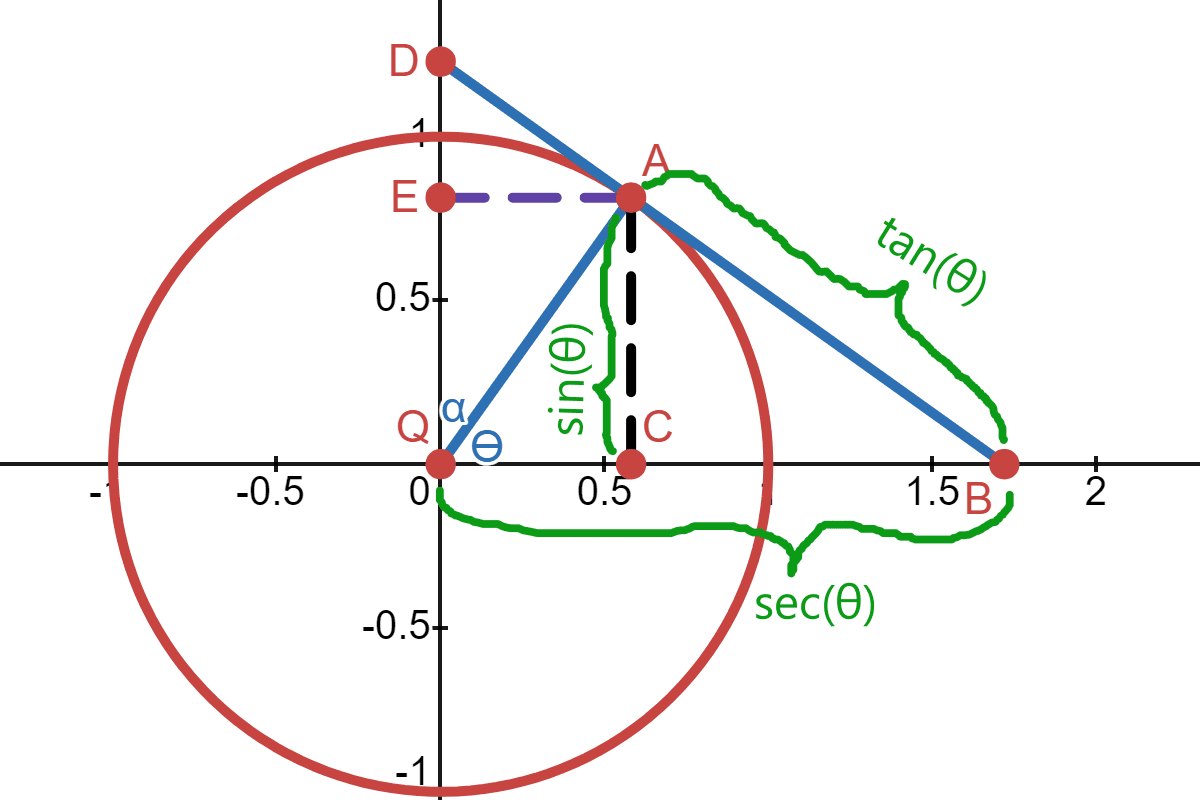
If the radius \(\overline{QA}\) were to be a different value, \(r\), other than 1, then \(\|\overline{AC}\|\) would be \(r\sin(θ)\), \(\|\overline{AB}\|\) would be \(r\tan(θ)\) and \(\|\overline{QB}\|\) would be \(r\sec(θ)\). In terms of opposite, adjacent and hypotenuse, they are defined as:
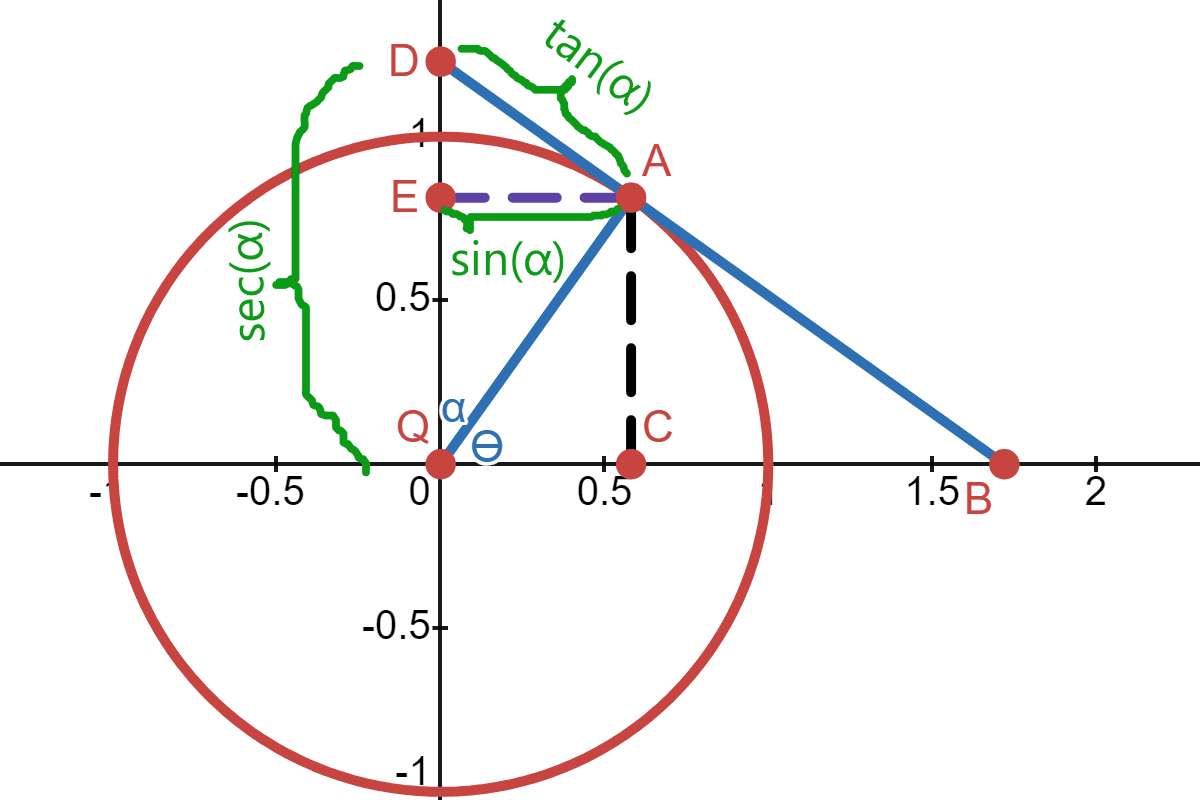
The angle \(\alpha\) is the angle between the radius \(\overline{QA}\) and the y-axis. \(\alpha\) and \(\theta\) are complementary angles (i.e. \(\alpha = 90 - \theta\)).
In the triangle \(QEA\), the line \(\overline{AE}\) is the line opposite of \(\alpha\), and the line \(\overline{QE}\) is the adjacent line. The function \(\sin (\alpha)\) is defined as the length of the opposite side \(\overline{AE}\) given that the hypotenuse is 1.
In the triangle \(QAD\), \(\overline{AD}\) is the opposite side, \(\overline{QA}\) is the adjacent side and \(\overline{QD}\) is the hypotenuse side. The function \(\tan (\alpha)\) is defined as the length of the tangent line \(\overline{AD}\) (i.e. the opposite side) given that the adjacent is 1. Also, the function \(\sec(\alpha)\) is defined as the hypotenuse side \(\overline{QD}\), given that the adjacent side is 1.
A function \(f\) is cofunction of a function \(g\) if \(f(A) = g(B)\) whenever \(A\) and \(B\) are complementary angles (pairs that sum to one right angle). This means \(\operatorname{cosine}(\alpha) = \operatorname{sine}(\theta)\), \(\operatorname{cosecant}(\alpha) = \operatorname{secant}(\theta)\) and \(\operatorname{cotangent}(\alpha)=\operatorname{tangent}(\theta)\):
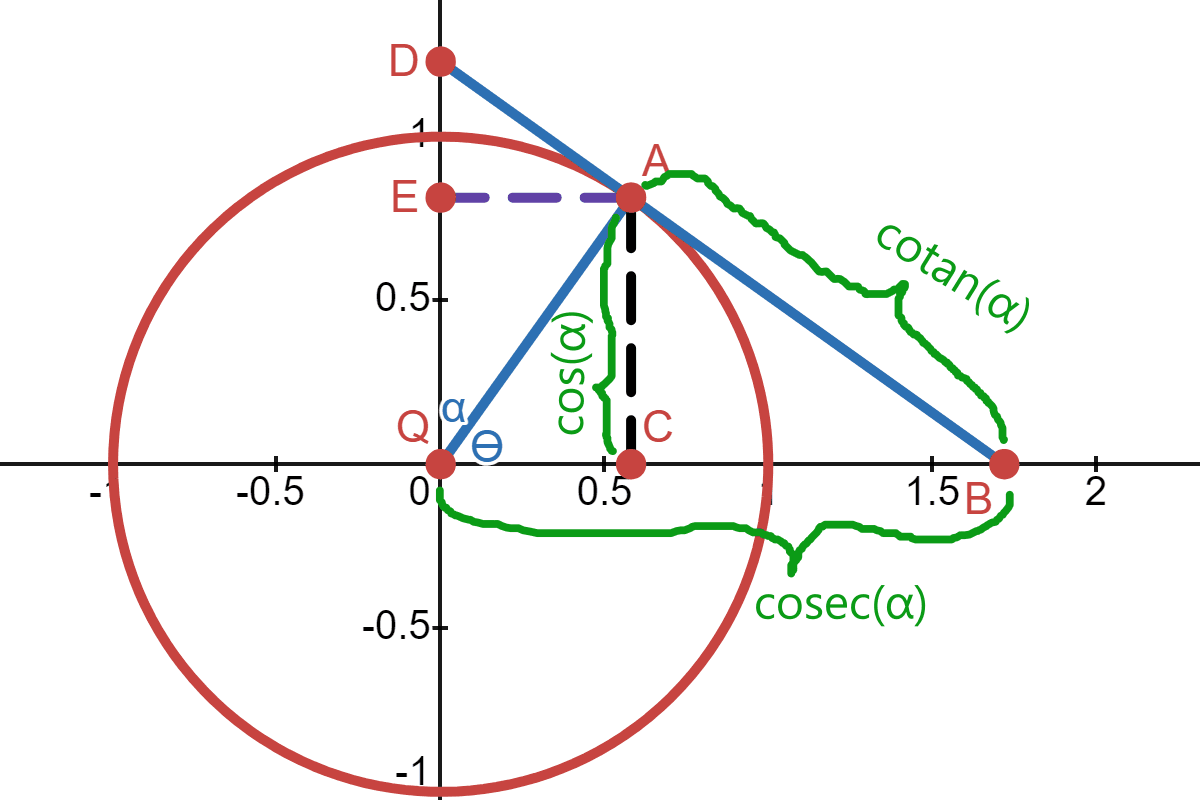
It also means \(\operatorname{cosine}(\theta) = \operatorname{sine}(\alpha)\), \(\operatorname{cosecant}(\theta) = \operatorname{secant}(\alpha)\) and \(\operatorname{cotangent}(\theta)=\operatorname{tangent}(\alpha)\):
So far we have learnt:
If the radius \(\overline{QA}\) were to be a different value, \(r\), other than 1, then \(\|\overline{AE}\|\) would be \(r\cos(θ)\), \(\|\overline{AD}\|\) would be \(r\cot(θ)\) and \(\|\overline{QD}\|\) would be \(r\csc(θ)\).
Since \(\angle QDA\) is \(\theta\) and \(\angle QAD\) is 90°, then in the triangle \(QAD\), \(\|\overline{QD}\|\) is the hypotenuse side, \(\|\overline{AD}\|\) is the adjacent side and \(\|\overline{QA}\|\) is the opposite side. Also, in the triangle \(QCA\), the line \(\overline{QC}\), which is the same length as \(\overline{AE}\), is the adjacent side. In terms of opposite, adjacent and hypotenuse, the three cofunctions are defined as:
This also means: