First lets start with a triangle with sides a, b and c. Using the pythagorean theorem, we know that a2, b2 and c2:
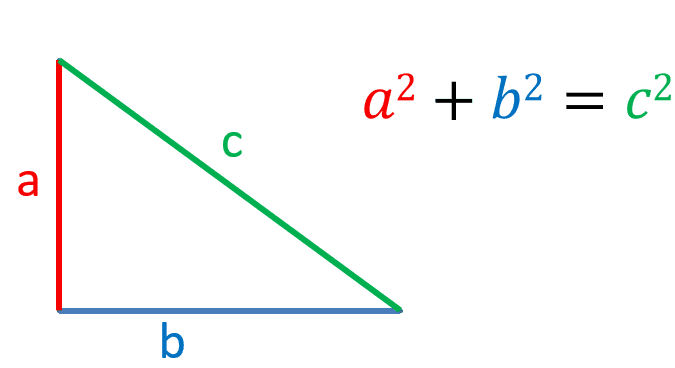
Lets say that there is an angle x; between line b and line c. In that case, line a would be the opposite side, line b would be the adjacent side and line c would be the hypotenuse:
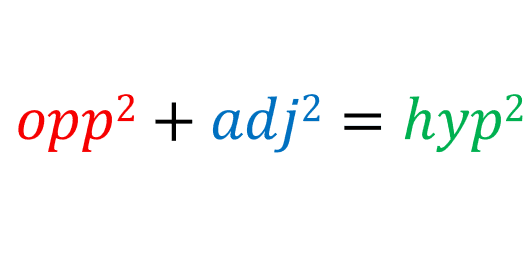
If we divide both sides by hypotenuse2, then:

Since cos(x) = adj/hyp and sin(x) = opp/hyp, then we can say that:
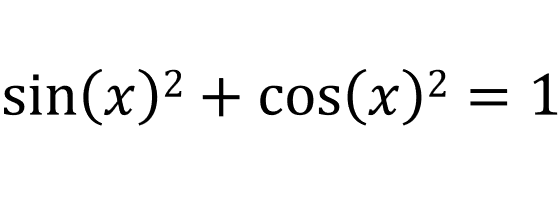
Let's go back to the Pythagorean theorem:
\[ \text{opp}^2 + \text{adj}^2 = \text{hyp}^2 \]
If we divide both side by \(\text{adj}^2\)
\[ \frac{\text{opp}^2}{\text{adj}^2} + \frac{\text{adj}^2}{\text{adj}^2} = \frac{\text{hyp}^2}{\text{adj}^2} \]
Simplify:
\[ \left( \frac{\text{opp}}{\text{adj}} \right) ^2 + 1 = \left( \frac{\text{hyp}}{\text{adj}} \right) ^2 \]
By using the trig definitions:
\[ \tan^2 (x) + 1 = \sec^2 (x) \]
Let's go back to the Pythagorean theorem again:
\[ \text{opp}^2 + \text{adj}^2 = \text{hyp}^2 \]
If we divide both side by \(\text{opp}^2\)
\[ \frac{\text{opp}^2}{\text{opp}^2} + \frac{\text{adj}^2}{\text{opp}^2} = \frac{\text{hyp}^2}{\text{opp}^2} \]
Simplify:
\[ 1 + \left( \frac{\text{adj}}{\text{opp}} \right) ^2 = \left( \frac{\text{hyp}}{\text{opp}} \right) ^2 \]
By using the trig definitions:
\[ 1 + \cot^2 (x) = \csc^2 (x) \]
The three Pythagorean identities we learnt is:
\[\begin{align} \sin^2(x) + \cos^2(x) &= 1 \\ \sec^2 (x) - \tan^2 (x) &= 1 \\ \csc^2 (x) - \cot^2 (x)&= 1 \end{align}\]