Proof Of The Addition Formulas And Subtraction Rule For sin(x)

You should already know the addition rule for cosine, if you don't then click here. The addition formula for cosine is written like this:

Since [cos(x) = sin(x + 90)], we can write:

Lets say [z = g - 90]:

We know that [cos(-x) = cos(x)] and that [-sin(-x) = sin(x)]:

Since [cos(90 - x) = sin(x)] and [sin(90 - x) = cos(x)], we can write:

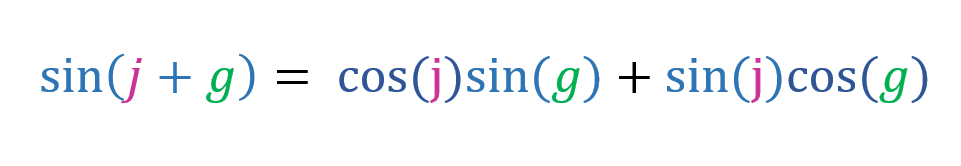
And that is the addition formula for sine. Now lets replace g with -v:

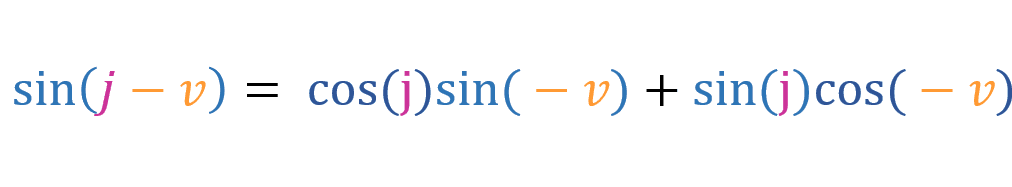
Since [cos(-v) = cos(v)] and [sin(-v) = -sin(v)], we can write the above equation like this:

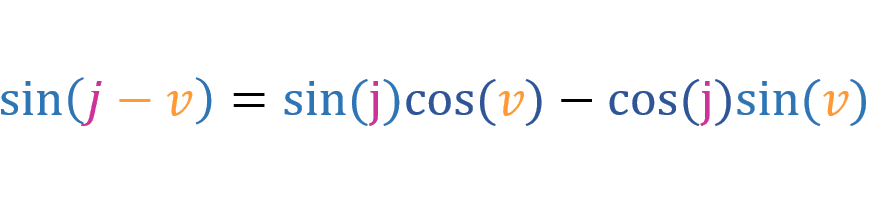
This is the subtraction rule for sine.