Deriving The Regression Coefficient Of y On x

Lets say we are given some x values with their associated y values:

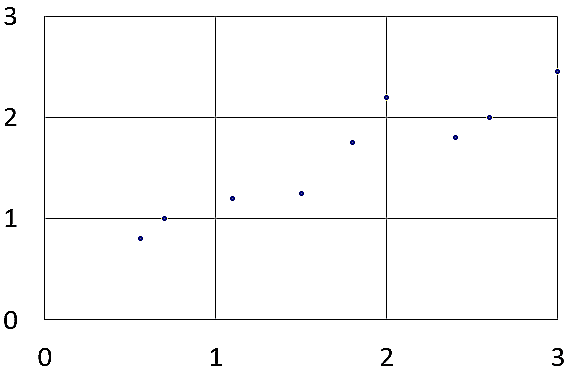
We can take a guess at what the best fit line could look like:

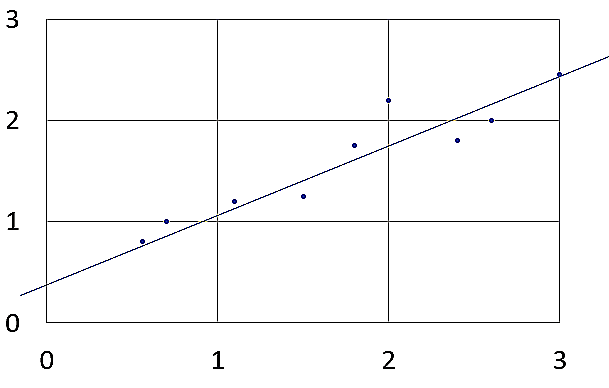
Let y_i be the output with x_i, and let h_i be the predicted output (= (θ * x_i) + α, where θ is the gradient of the best fit line and α is the bias).

We will introduce another variable: loss, which is the sum of (y_i - h_i)².

The smaller the difference between y_i and h_i, the smaller the value of loss. Our goal is to find the θ which will give the smallest possible value for loss. We can start by differentiating the loss with respect to θ, but before we do that, we must first expand α:

In the above equation, y_m represents the mean y value, and x_m represents the mean x value. The line of best fit is expected to pass through (x_m, y_m), meaning y_m = θx_m + α. Now lets differentiate the loss:

With different values of θ, we get different values of loss. The loss function (with respect to θ) is a parabola, and to find the global minimum, we can set the gradient to 0.

We can simplify this:

Now lets make θ the subject:

This will give us the regression coefficient: