Let vectors \(\textbf{v}\) and \(\textbf{u}\) be defined as follows:
$$ \textbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \quad \textbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} $$
The dot product \(\textbf{v} \cdot \textbf{u}\) is defined as follows:
$$ \textbf{v} \cdot \textbf{u} = v_1u_1 + v_2u_2 + v_3u_3 $$
This is the component-wise definition. Let the angle between the vectors be \(\theta \lt 90^{\circ}\):
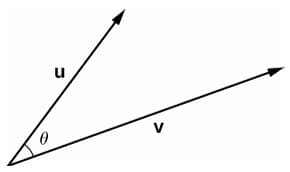
This means \(\textbf{v}\), \(\textbf{u}\), \(\textbf{v}-\textbf{u}\) can form a triangle:
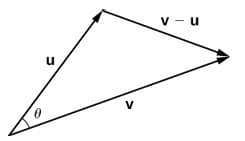
According to the cosine rule from trigonometry:
$$ \Vert \textbf{v} - \textbf{u} \Vert^2 = \Vert \textbf{v} \Vert^2+ \Vert \textbf{u} \Vert^2 -2(\Vert \textbf{v} \Vert \ \Vert \textbf{u} \Vert) \cos(\theta) $$
Since the square of a vector's magnitude is the dot product of that vector with itself:
$$ \Vert \textbf{v} - \textbf{u} \Vert^2 ={\color{red} (\textbf{v} - \textbf{u} )} \cdot {\color{green}(\textbf{v} - \textbf{u})} $$
According to the distributive property:
$$\begin{align} \Vert \textbf{v} - \textbf{u} \Vert^2 &= ({\color{red} (\textbf{v} - \textbf{u} )} \cdot {\color{green}\textbf{v}}) - ({\color{red} (\textbf{v} - \textbf{u} )} \cdot {\color{green}\textbf{u}}) \\ &= \textbf{v}\cdot \textbf{v} - \textbf{u} \cdot \textbf{v} -\textbf{v} \cdot \textbf{u}+ \textbf{u}\cdot\textbf{u} \\ &= \Vert \textbf{v} \Vert ^2- 2\textbf{u} \cdot \textbf{v} + \Vert \textbf{u}\Vert^2\end{align}$$
This means:
$$\begin{align} \Vert \textbf{v} - \textbf{u} \Vert^2 &= \Vert \textbf{v} \Vert^2+ \Vert \textbf{u} \Vert^2 -2(\Vert \textbf{v} \Vert \ \Vert \textbf{u} \Vert) \cos(\theta) \\ \Vert \textbf{v} \Vert ^2- 2\textbf{u} \cdot \textbf{v} + \Vert \textbf{u}\Vert^2 &= \Vert \textbf{v} \Vert^2+ \Vert \textbf{u} \Vert^2 -2(\Vert \textbf{v} \Vert \ \Vert \textbf{u} \Vert) \cos(\theta)\end{align} $$
Cancelling out like terms:
$$- 2\textbf{u} \cdot \textbf{v} = -2(\Vert \textbf{v} \Vert \ \Vert \textbf{u} \Vert) \cos(\theta) $$
Dividing both sides by -2:
$$ \textbf{u} \cdot \textbf{v} = \Vert \textbf{v} \Vert \ \Vert \textbf{u} \Vert \ \cos(\theta) $$