Let vectors \(\textbf{a}\) and \(\textbf{b}\) be defined as follows:
$$ \textbf{a} = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} \quad \textbf{b} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} $$
Let \(\textbf{w}\) be the cross product of \(\textbf{a} \times \textbf{b}\):
$$\begin{align} w_1 &= a_2 b_3 - a_3b_2 \\ w_2 &= -(a_1 b_3 - a_3b_1) \\ w_3 &= a_2b_1 - a_1b_2 \end{align}$$
You can use the right-hand rule to remember the orientation.
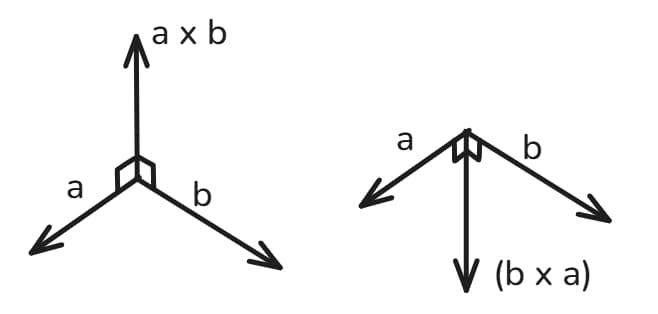
Multiplying a vector by -1 gives the vector of the same magnitude but in the opposite direction:
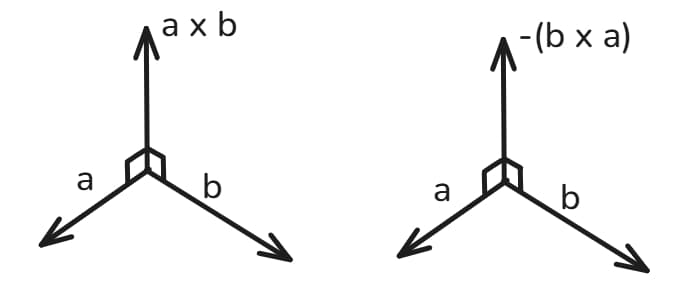
If you want an algebraic proof, we can define a vector \(\textbf{v}\) that is the cross product \(\textbf{b} \times \textbf{a} \):
$$\begin{align} v_1 &= b_2 a_3 - b_3a_2 \\ v_2 &= -(b_1 a_3 - b_3a_1) \\ v_3 &= b_2a_1-b_1a_2 \end{align}$$
If we multiply by -1:
$$\begin{align} -v_1 &= b_3a_2 - b_2 a_3 \\ -v_2 &= -(b_3a_1 - b_1 a_3) \\ -v_3 &= b_1a_2-b_2a_1 \end{align}$$
The components of \(-\textbf{v}\) is the same as \(\textbf{w}\).