Proof That Two Lines Are Perpendicular If The Gradient Of One Line Is The Negative Reciprocal Of The Other

Suppose we have a right-angled triangle \(T_1\), with base \(b\) and height \(h\). We will draw this triangle on a graph, which is made from three points: \((0,0)\), \((0,h)\) and \((b,0)\):

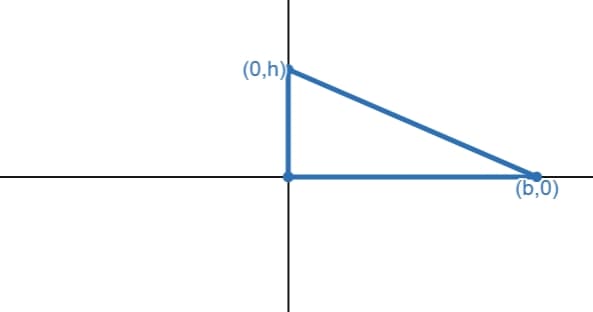
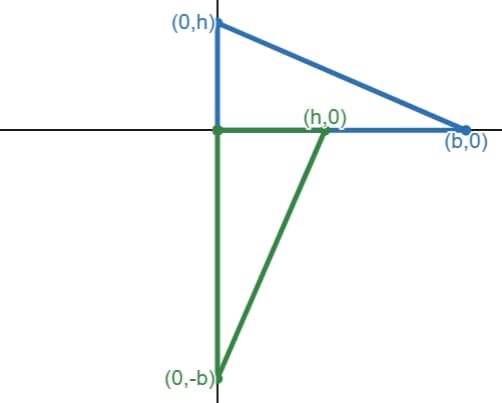
Suppose we rotate this triangle \(90^ \circ\) clockwise around the origin, so the triangle is now in the fourth quadrant. Let's call this rotated triangle \(T_2\):

The corner points of \(T_2\) is \((0,0)\), \((0,-b)\) and \((h,0)\).

Consider hypotenuses of \(T_1\) and \(T_2\). Let's call them \(c_1\) and \(c_2\) (note that these are line segments):

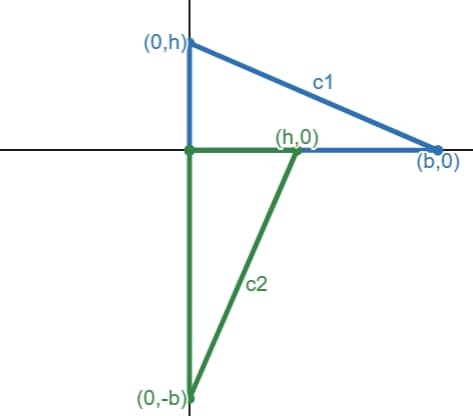
All sides in \(T_2\) is perpendicular to the corresponding side of \(T_1\). For example, The ilne segments \(c_1\) and \(c_2\) are perpendicular. The gradient of \(c_1\) is:

$$ \text{gradient of } c_1 = \frac{\text{rise}}{\text{run}} = \frac{h}{b} $$

The gradient of \(c_2\) is:

$$ \text{gradient of } c_2 = \frac{\text{rise}}{\text{run}} = \frac{-b}{h} $$

The gradient of one line segment is the negative reciprocal of the other.

Another proof involves the dot product of two vector. Consider these two vectors:

$$ \begin{gather} \textbf{u} = \langle 1,k_1 \rangle \\ \textbf{v} = \langle 1,k_2 \rangle \end{gather}$$

Both of these vectors go only one unit in the \(x\) direction. If these two vectors are orthogonal, then their dot product should be zero:

$$ \textbf{u} \cdot \textbf{v} = \Vert \textbf{u} \Vert \ \Vert \textbf{v} \Vert \cos(90^\circ) = 0$$

Using the other definition of dot product:

$$\begin{gather} \textbf{u} \cdot \textbf{v} = 1 + k_1k_2 \\ \therefore 0 = 1 + k_1 k_2 \end{gather}$$

Since \( k_1 k_2 = -1\), then the "rise" of one vector over one unit increment in the \(x\) direction (called \(k_1\)) should be the negative reciprocal of the "rise" of the other vector \((k_2)\):

$$ k_1 = - \frac{1}{k_2} $$