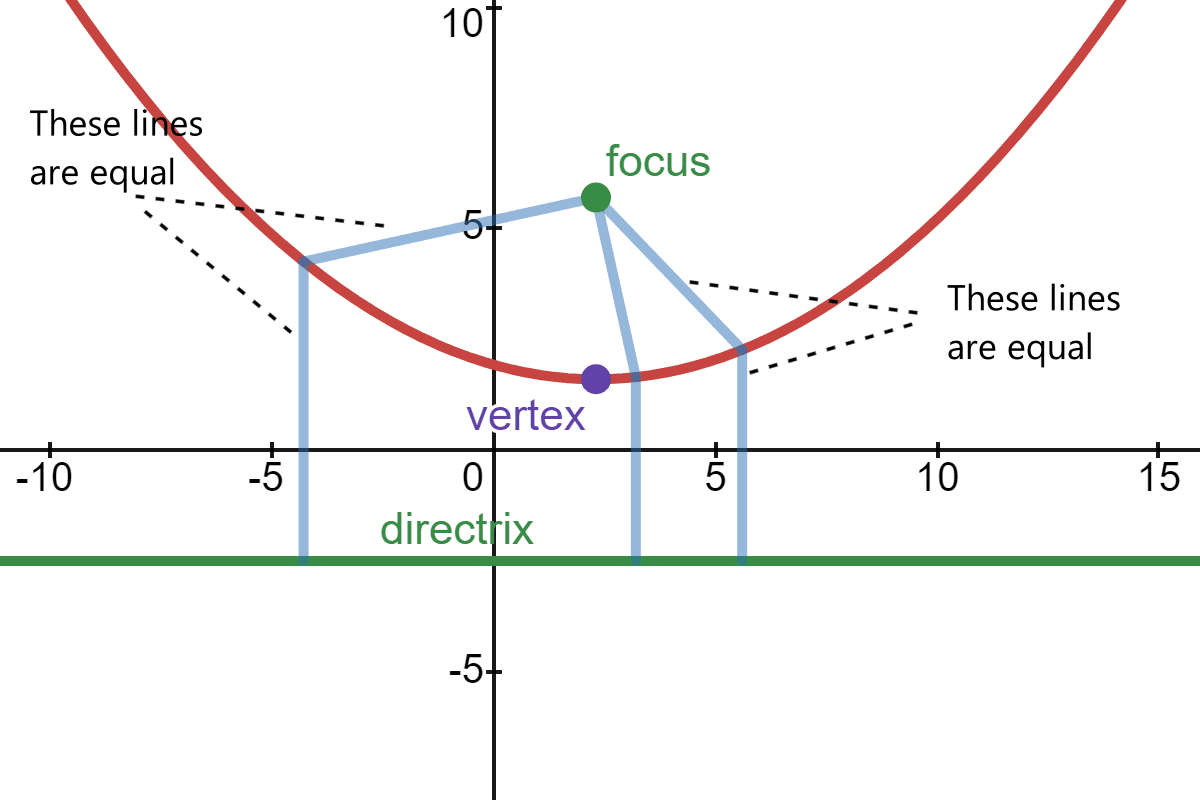
The parabola is defined as the set of all the points that are equidistant from the focus and directrix. The point halfway between the focus and the directrix is called the vertex of the parabola:

By definition, a line from the focus to a point in a parabola, and a line from the same point to the directrix are equal in length:
For simplicity, we will work with a parabola which has a vertex at the origin. Let's choose a point on the parabola (black point):
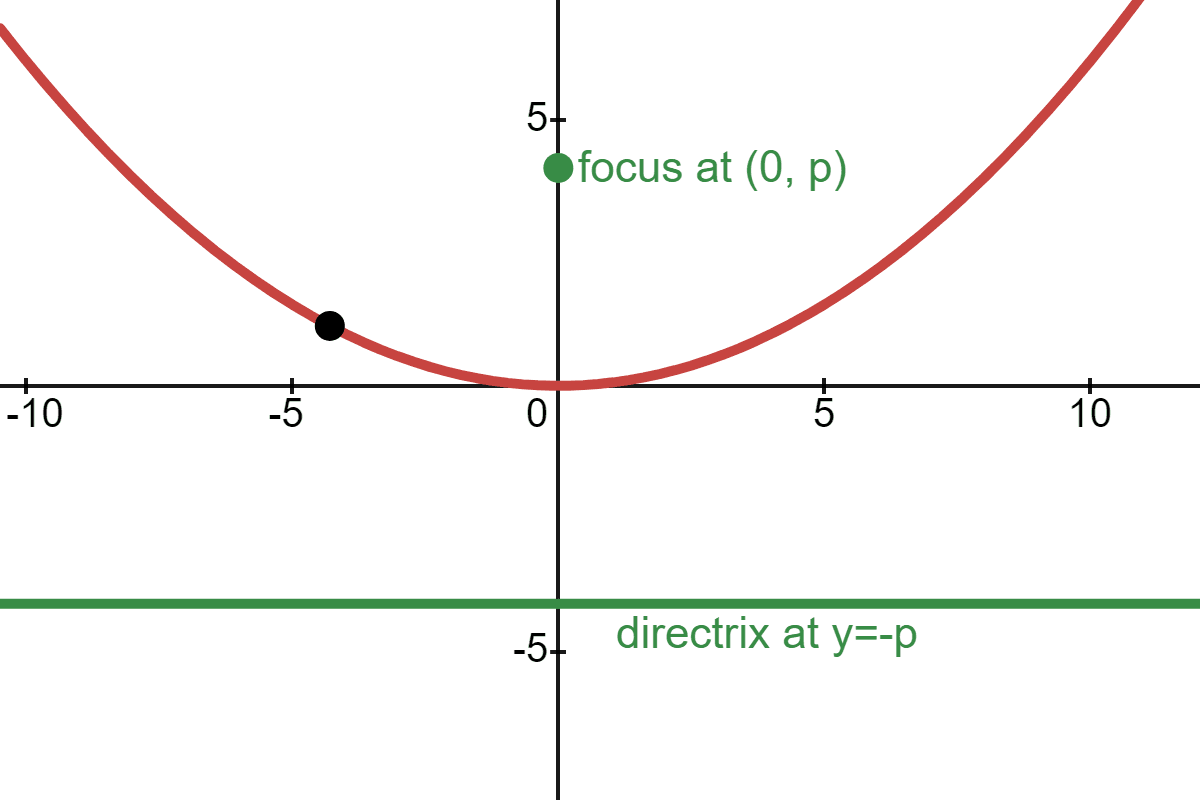
The distance from our point to the focus is equal to the distance from our point to the directrix:
Expanding and simplifying:
This means:
If the parabola is shifted upwards by \(k\) units, then the equation becomes:
If the parabola is shifted to the right by \(h\) units, then the equation becomes:
This is a vertex form equation of a parabola.
