The vertex form equation of a parabola is:
\[ y=\frac{(x-h)^2}{4p} + k\]
The vertex is at \((h,k)\), the focus is at \((h,k+p)\) and the directrix is the line \((h,k-p)\). If the parabola is represented in the standard form \(y=ax^2+bx+c\), then how can we derive the vertex, focus and directrix? In this article, we show that \(a= \frac{1}{4p}\), we can use this to get \(p\) from \(a\). We can also get \(h\) from \(b=-\frac{h}{2p}\).
The axis of symmetry is \(x=\frac{-b}{2a}\). This means the vertex is at \((-\frac{b}{2a}, k)\).
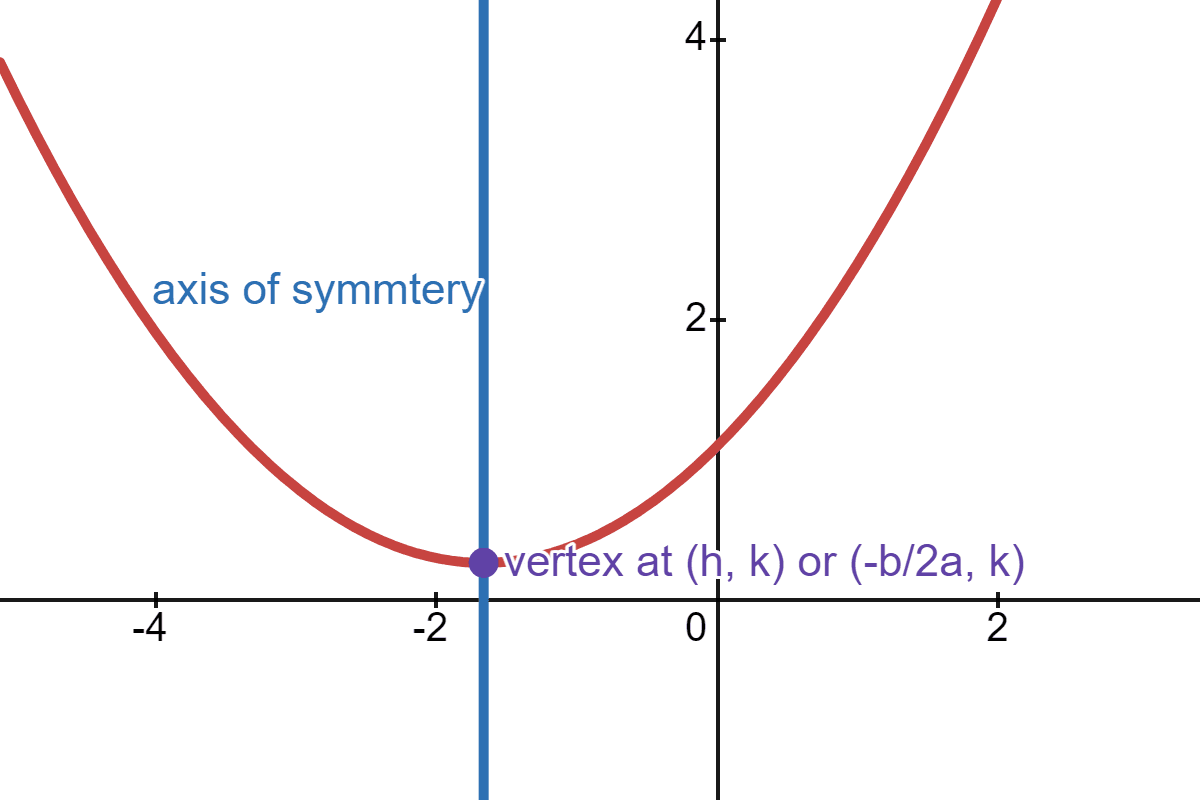
We can get \(k\) from \(c = \frac{h^2}{4p} +k\):
\[\begin{gather} c = \frac{h^2}{4p} +k = ah^2 + k = a \left( \frac{-b}{2a} \right)^2 +k = \left( \frac{b^2}{4a} \right) +k\\ \therefore k = c- \left( \frac{b^2}{4a} \right)\end{gather}\]
Knowing this, we can then get the focus using and directrix:
\[\begin{align} \text{focus: } & (h,k+p) = \left( \frac{-b}{2a}, c- \left( \frac{b^2-1}{4a} \right) \right) \\ \text{directrix: } & (h,k-p) = \left( \frac{-b}{2a}, c- \left( \frac{b^2+1}{4a} \right) \right) \end{align}\]