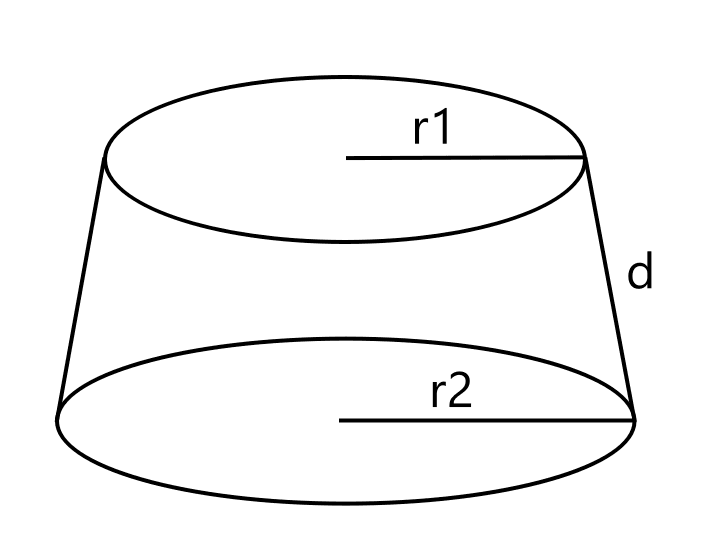
Imagine a right circular cone with two planes parallel to the cone's base cutting the cone. A right circular conical frustrum is the portion of a solid the lies between two parallel planes:

When the two planes intersect the cone, the intersection is a circle. Let \(r_1\) be the radius of the smaller circle, \(r_2\) be the radius of the larger circle and \(d\) be the slant height of the frustrum:
Let \(s\) be the slant height from \(r_2\) to the apex of the cone:
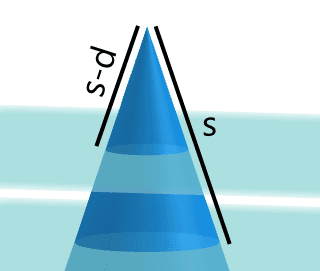
The lateral surface area of the frustrum is the lateral surface area of the larger cone with slant height \(s\) minus the lateral surface area of the smaller cone with slant height \(s-d\):
Let's find a way to get rid of \(s\). We can start with:
If we make \(s\) the subject:
We can simplify this:
Since \((r_2^2+r_1^2) = (r_2+r_1)(r_2-r_1)\):