Here is a right circular cone (laying down) with height \(h\) and the radius of it's circular base \(r\) that rolled from point \(A\) to \(B\):
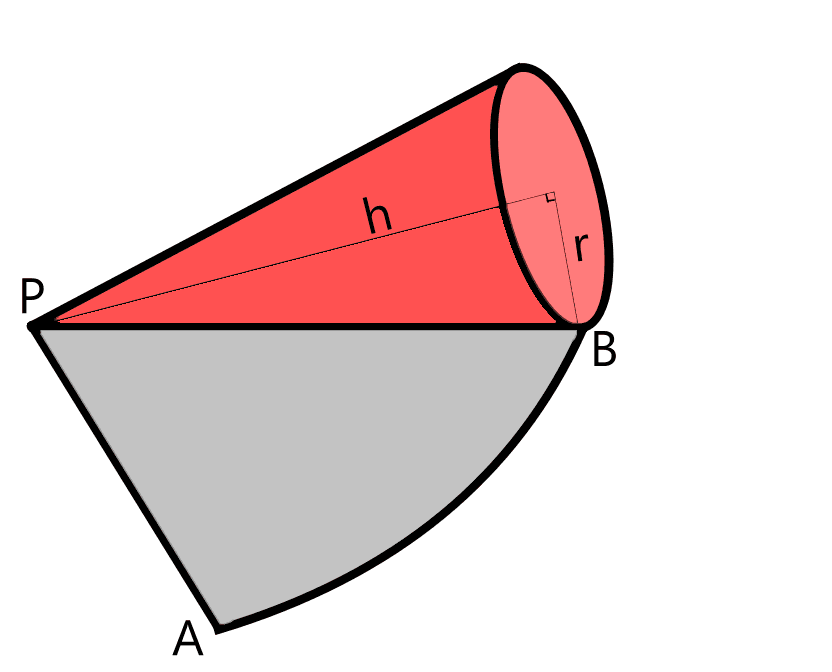
Point \(P\) is the apex of the cone. The cone did one full roll from point \(A\) to \(B\). The gray area represents the region the cone covered during that full roll. This means the arc length of the gray area from \(A\) to \(B\) is the same of the circumference of the cone's circular base. It also means that the surface area of the gray area is the same as the lateral surface area of the cone, so to calculate the lateral surface area, you just have to calculate the area of the gray region.
Since every point on the arc length is equidistant from point \(P\), that means the gray region is a sector of a circle:
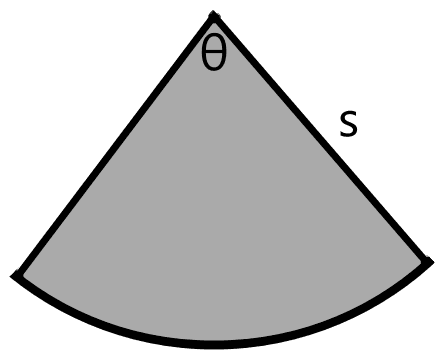
Let \(\theta\) be the central angle in radians, and let \(s\) be the radius of the sector. This means that \(s\) is also the slant height of the cone:
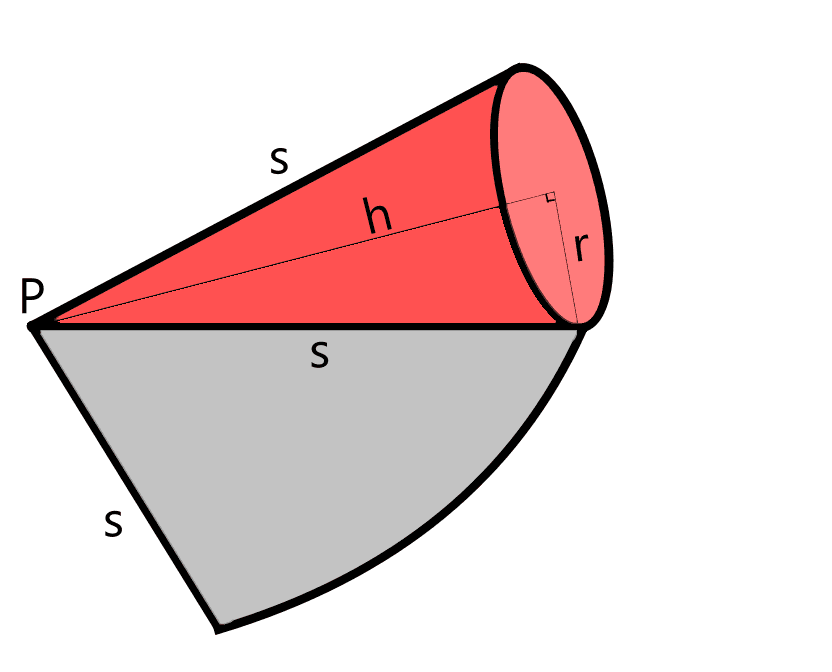
The arc length can be calculated in two ways, one by using the cone's base, and the other by using the gray sector:
The surface area of the gray region is:
Therefore, the lateral surface area of the cone is \(\pi s r\) where \(r\) is the radius of the base and \(s\) is the slant height.