(Hyperbola) Deriving the standard form equation

Suppose we have a hyperbola with the center \((0,0)\):

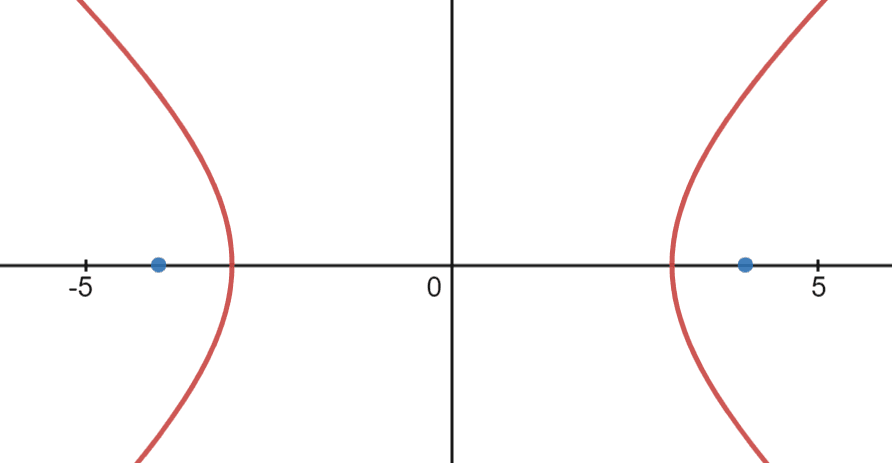
A hyperbola is a set of points, such that for any point \(P\) of the set, the absolute difference in the distances from point \(P\) to the two foci (shown in blue) is constant:

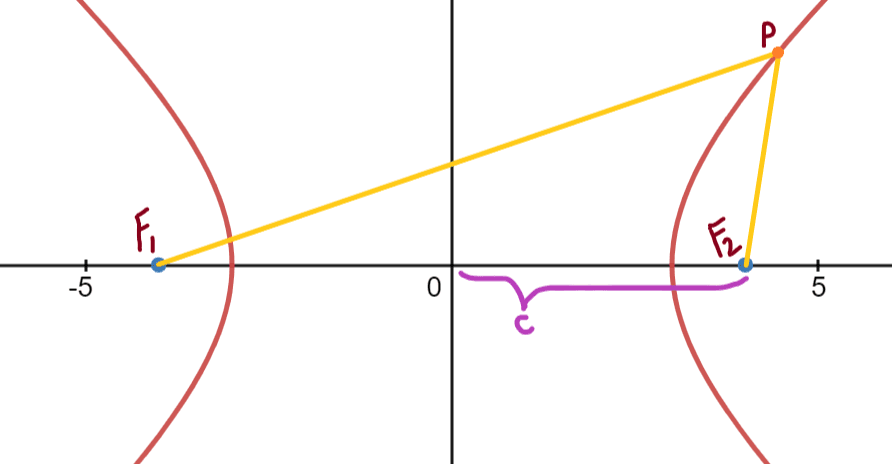
Let's call the shortest distance from the origin to either of the foci \(c\):

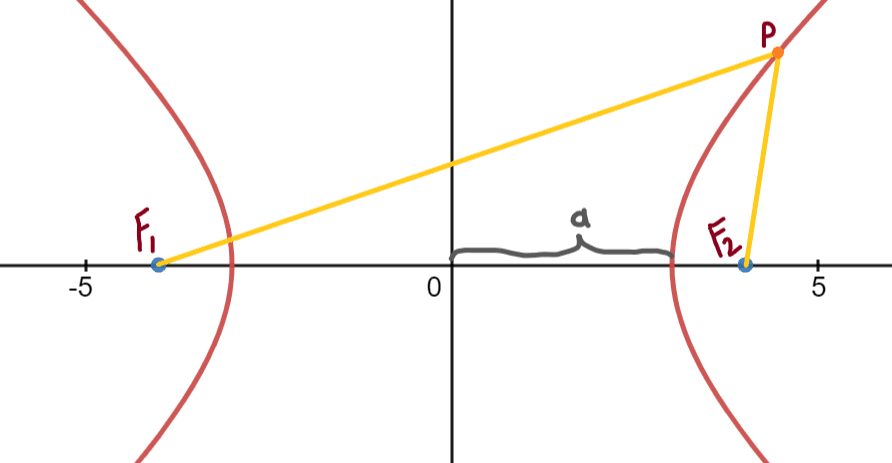
Let's call the shortest distance from the origin to either of the hyperbola line \(a\):

The absolute difference between \(|PF_1|\) and \(|PF_2|\) is \(2a\). Let \(P\) be at \((p_x,p_y)\), \(F_1\) be at \((f_{1x}, 0)\) and \(F_2\) be at \((f_{2x},0)\). Now let's define another point \(A = (p_x,0)\), where \(\angle PAF_{1x} = 90^\circ \):

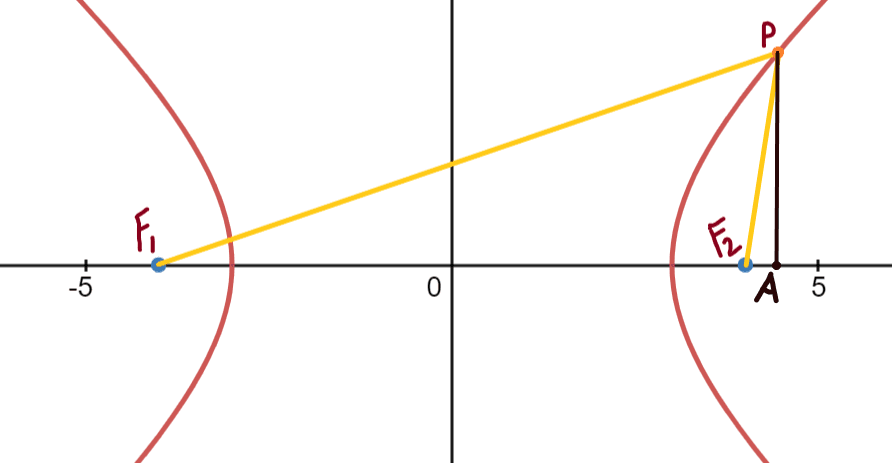
If we use the Pythagorean theorem:

\[|PF_1|=\sqrt{(p_x-f_{1x})^2+(p_y)^2}\] \[|PF_2|=\sqrt{(p_x-f_{2x})^2+(p_y)^2}\]

Since \(|PF_1|-|PF_2|=2a\):

\[\sqrt{(p_x-f_{1x})^2+(p_y)^2} - \sqrt{(p_x-f_{2x})^2+(p_y)^2} = 2a\]

Since \(c=f_{2x}=-f_{1x}\):

\[\sqrt{(p_x+c)^2+(p_y)^2} - \sqrt{(p_x-c)^2+(p_y)^2} = 2a\]

Rearranging:

\[\sqrt{(p_x+c)^2+(p_y)^2} = 2a + \sqrt{(p_x-c)^2+(p_y)^2}\] \[(p_x+c)^2+(p_y)^2 = 4a^2 + 4a \sqrt{(p_x-c)^2+(p_y)^2} + (p_x-c)^2 + (p_y)^2 \]

We can cancel \((p_y)^2\) and then simplify:

\[(p_x)^2+2p_xc+c^2 = 4a^2 + 4a \sqrt{(p_x-c)^2+(p_y)^2} + (p_x)^2 -2p_xc + c^2 \] \[p_xc = a^2 + a \sqrt{(p_x-c)^2+(p_y)^2}\]

We can square both side:

\[p_xc - a^2= a \sqrt{(p_x-c)^2+(p_y)^2}\] \[(p_xc - a^2)^2= a^2(p_x-c)^2+ a^2(p_y)^2\]

Expand:

\[(p_x)^2c^2 - 2p_xca^2 + a^4= a^2((p_x)^2-2p_xc+c^2)+ a^2(p_y)^2\] \[(p_x)^2c^2 - 2p_xca^2 + a^4 = a^2(p_x)^2-2p_xca^2+a^2c^2+ a^2(p_y)^2\]

Simplify:

\[(p_x)^2c^2 + a^4 = a^2(p_x)^2+a^2c^2+ a^2(p_y)^2\]

Rearrange and simplify further:

\[(p_x)^2c^2 - a^2(p_x)^2 - a^2(p_y)^2 = a^2c^2 - a^4\] \[(p_x)^2(c^2 - a^2) - a^2(p_y)^2 = a^2(c^2 - a^2)\]

This gives us our equation for a hyperbola:

\[\frac{(p_x)^2}{a^2} - \frac{(p_y)^2}{(c^2 - a^2)} = 1\]

You can view this in desmos. If you set \(c=0\), you get a circle, and if you set \(c \lt a\), then you get an ellipse. Also, if both the denominators are 1, then you get something called a unit hyperbola:

\[(p_x)^2 - (p_y)^2 = 1\]

Deriving The Standard Form Equation From The Geometric Definition