The definition of an hyperbola is the set of all points for which the absolute difference of their distances from two fixed points (the foci) is constant. Consider a hyperbola where the centre is at the origin:
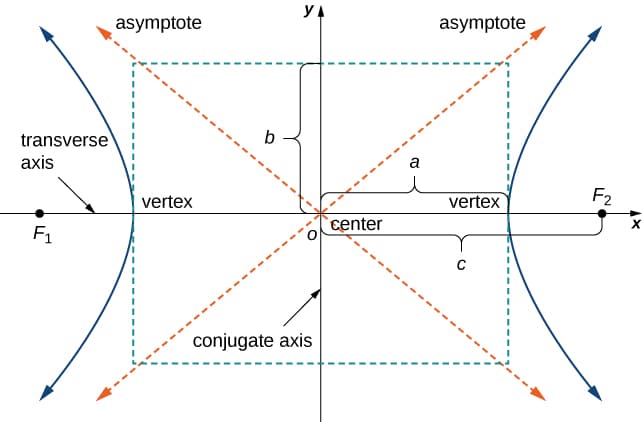
Choose any point \(P=(x_p, y_p)\) on right side of the hyperbola. \(x_p\) and \(y_p\) satisfies:
Assume that the distance from any point \(P\) to a focus \(F\) divided by the distance from \(P\) to a fixed line \(L\) (called the directrix) is contant. Let the directrix be at \(x=x_d\) for some \(x_d < a\).
\(F=(c,0)\), and \(P\) is a point of our choice. If \(P\) is on the \(x\)-axis (i.e. \(y_p=0\) and \(x_p=a\)), then the distance from \(F\) to \(P\) would be \(c-a\), and the distance from \(P\) to the directrix is \(a-x_d\). We already know that the eccentricity is \(\frac{c}{a}\). Therefore:
This means the directrix is at \(x_d = \frac{a^2}{c}\):
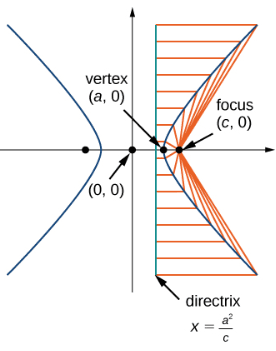
Since this hyperbola is symmetric along the \(y\)-axis, then there is another directrix at \(x_d = -\frac{a^2}{c}\). Also, if you shift the hyperbola \(h\) units to the right, then the directrix would be \(x_d = h±\frac{a^2}{c}\).