Consider an ellipse where the centre is at the origin and choose of point \(A\) that lies on the ellipse:
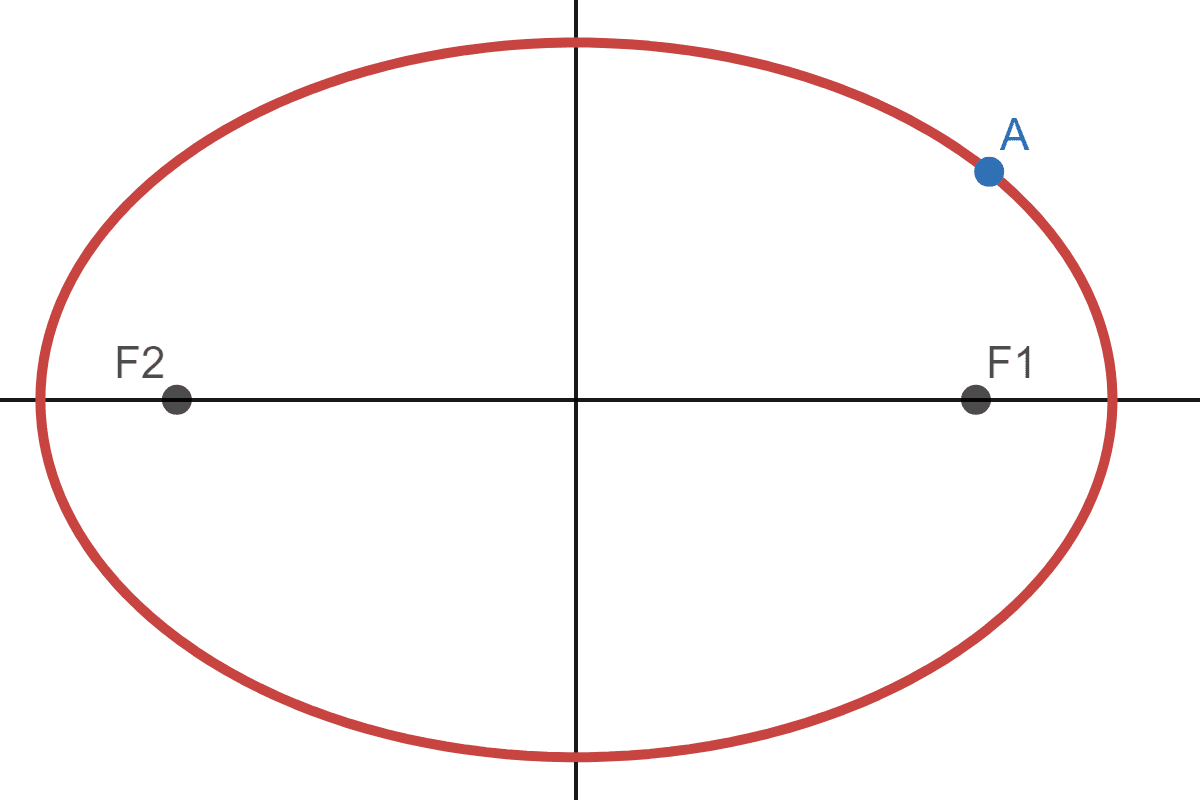
The point \(F_1\) is the left focus while \(F_2\) is the right focus. Now imagine a tangent line at \(A\):
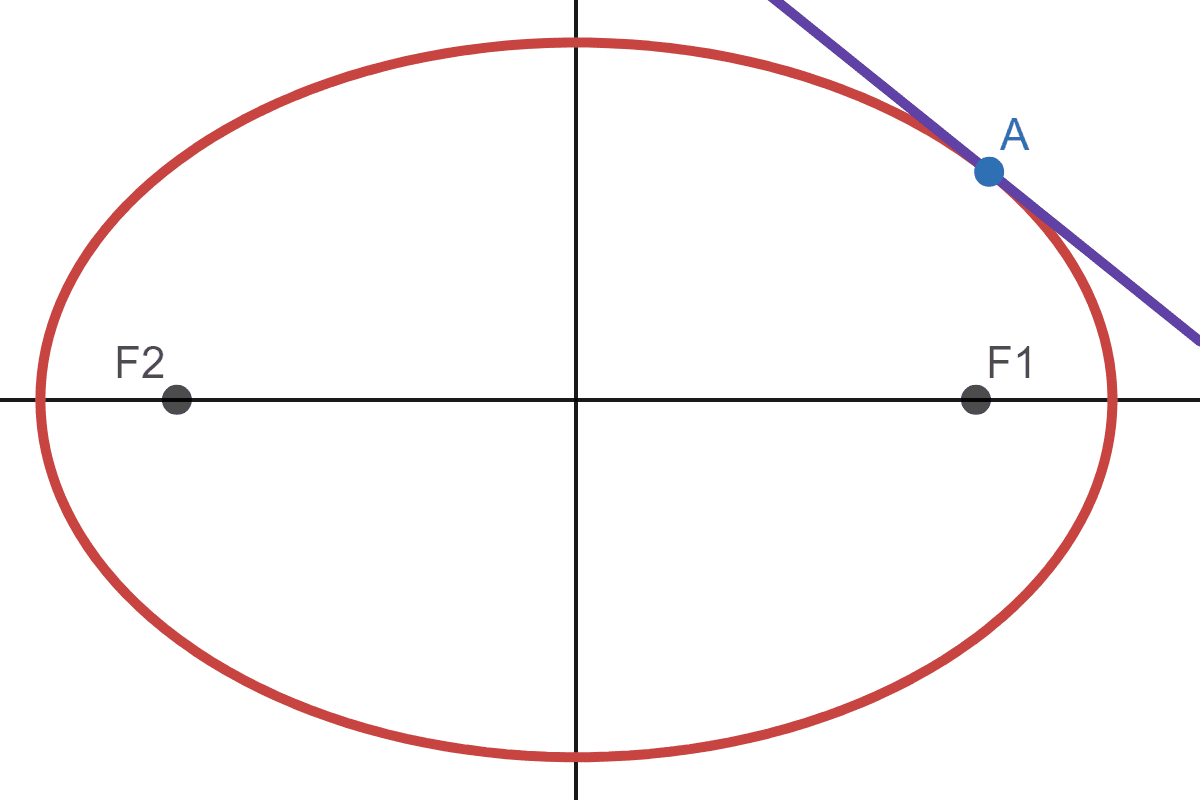
Let the tangent line act as a mirror, and let \(F_1^*\) be the image of \(F_1\):
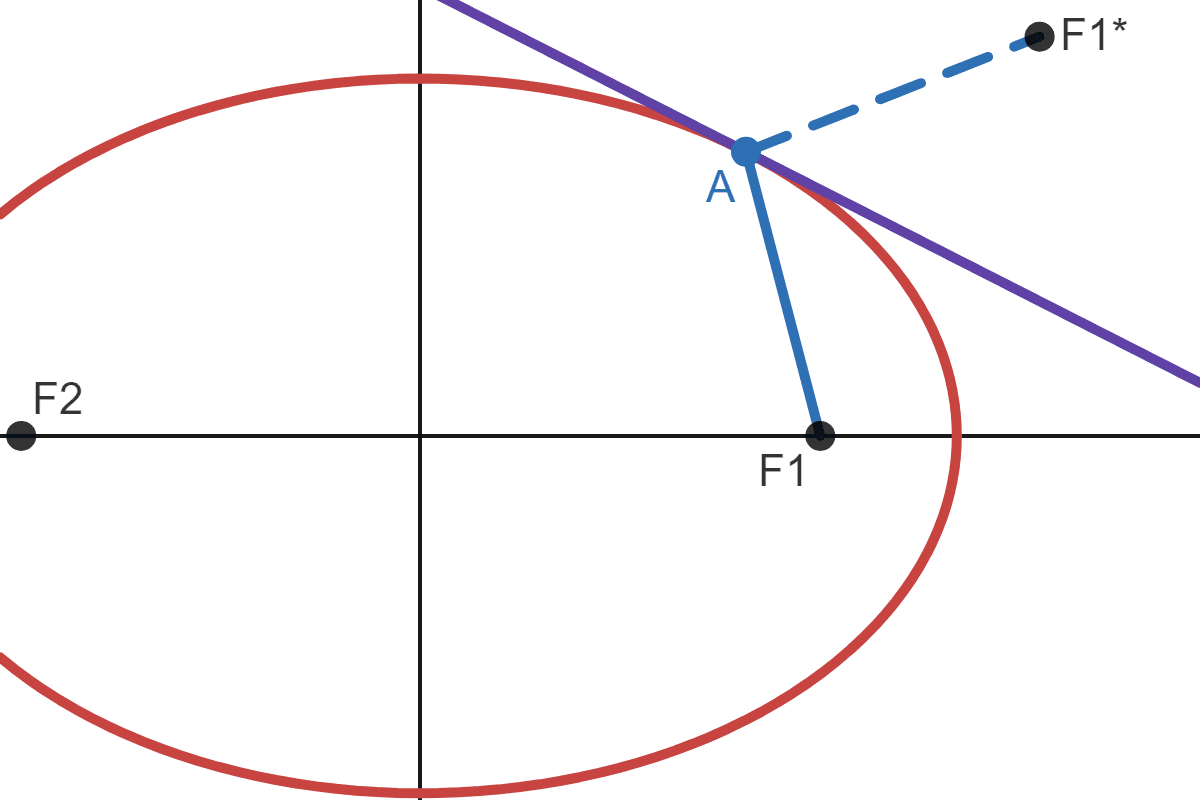
The blue line goes from \(F_1\) to \(A\), and the dashed line is the mirror image of the blue line, so it goes from \(A\) to \(F_1^*\). According to the reflective property, if the blue line is reflected off the ellipse, it should meet the other focus. If that were to be true, then \(F_2\), \(A\) and \(F_1^*\) would form a straight line:
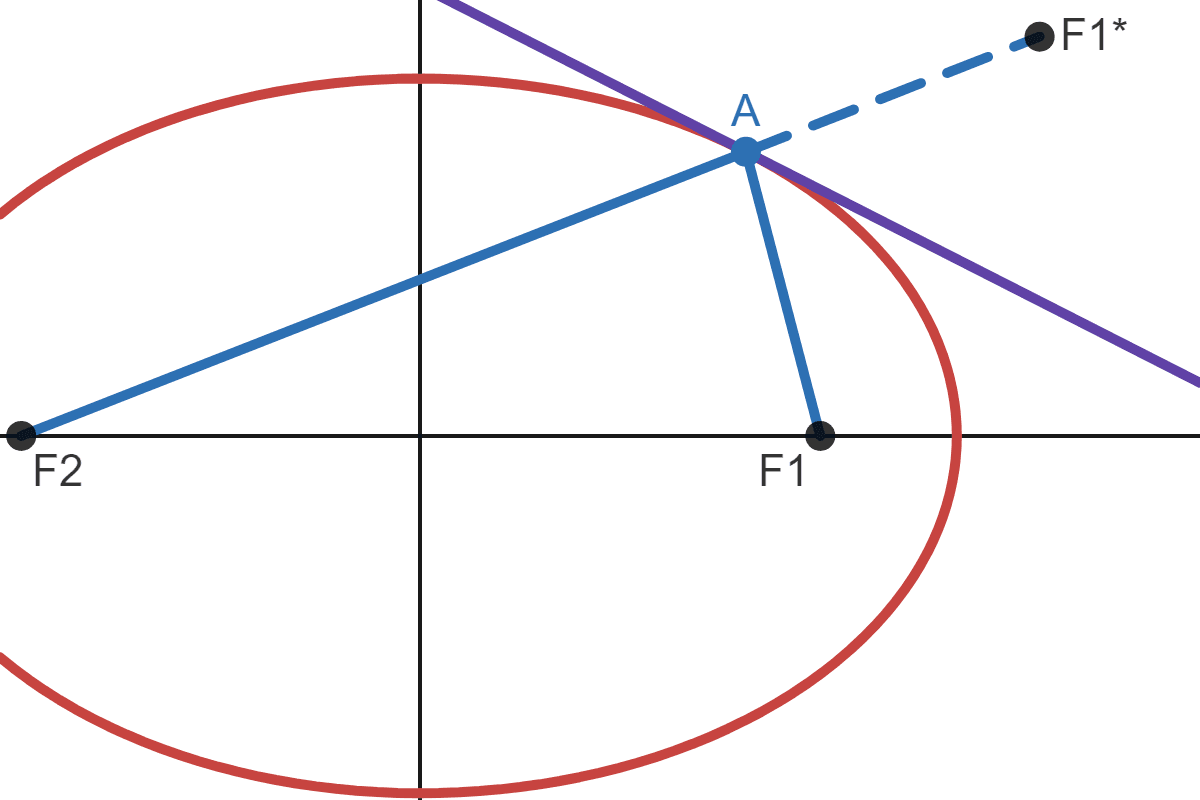
Since \(\Vert F_2 \ A \Vert + \Vert A \ F_1 \Vert = 2a\), then \(\Vert F_2 \ A \Vert + \Vert A \ F_1^* \Vert = 2a\). How do we prove that for any point \(A\), points \(F_2\), \(A\) and \(F_1^*\) would form a straight line?
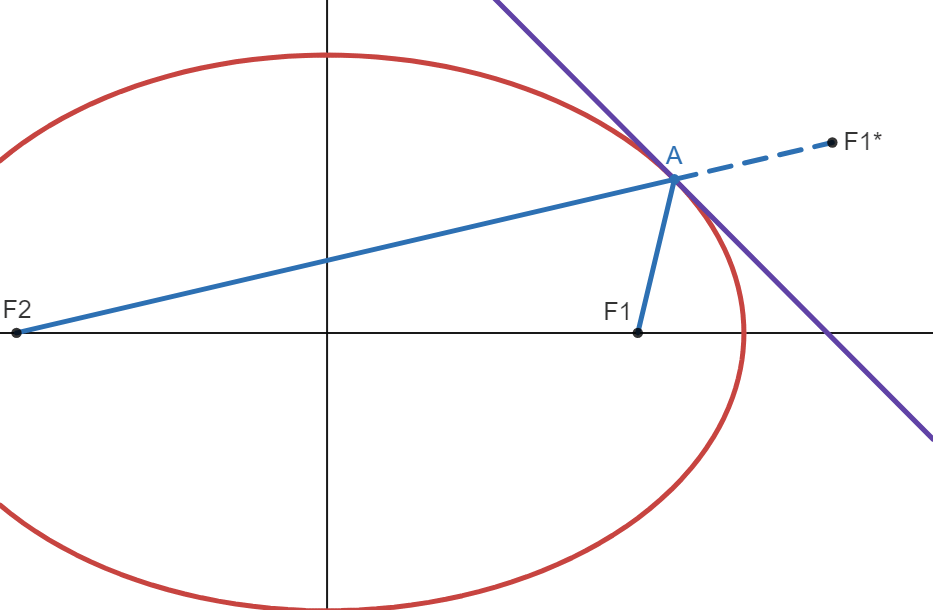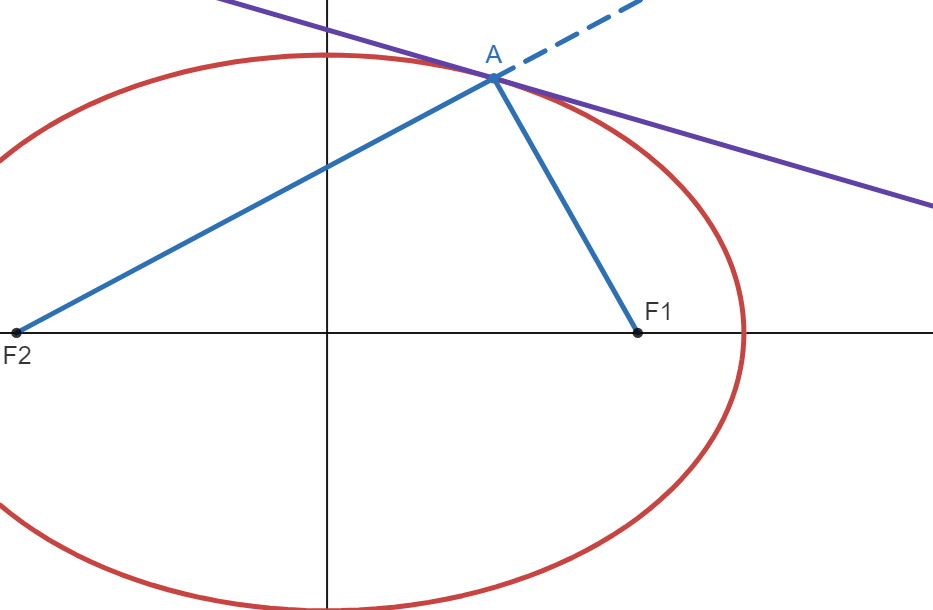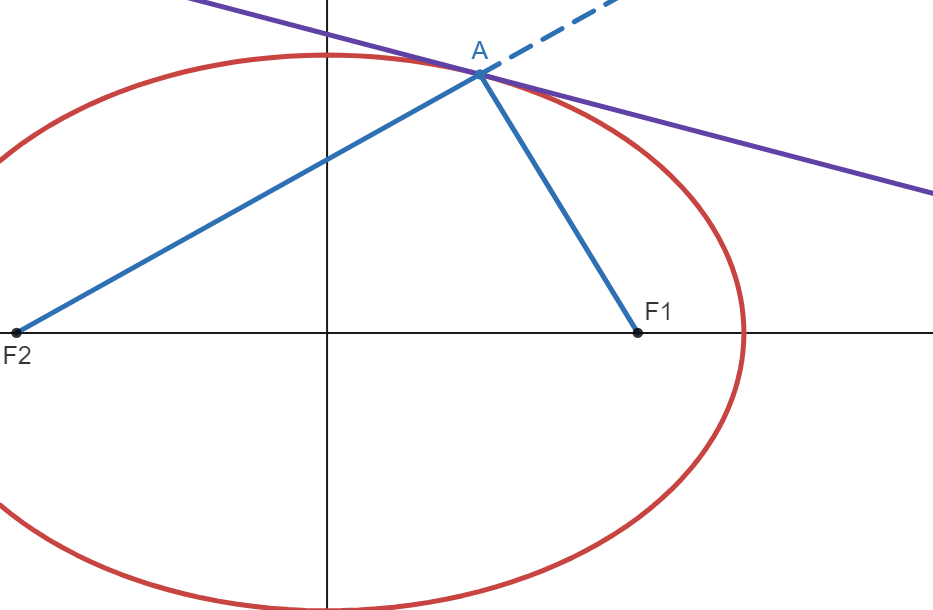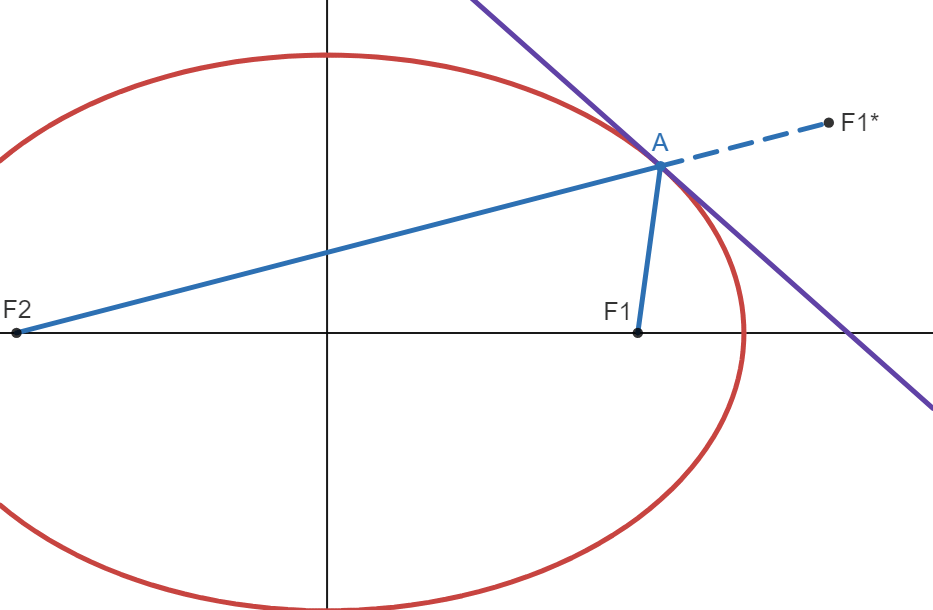
We can try proof by contradiction. Let's say the image \(F_1^*\) does not lie on the line \(\scriptstyle{\overleftrightarrow{F_2 \ A}}\), even though \(\Vert F_1 \ A \Vert = \Vert A \ F_1^* \Vert\):
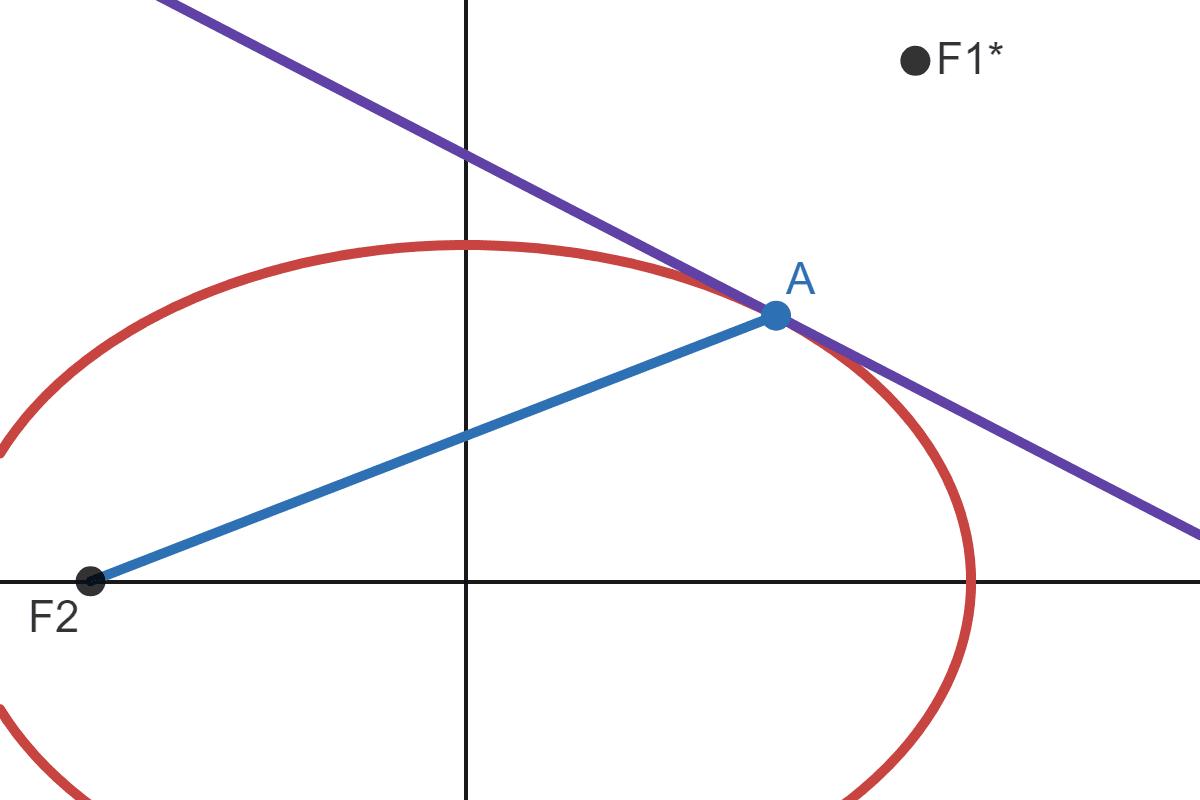
This means \(F_2\), \(A\) and \(F_1^*\) would form a triangle, and according to the triangle inequality theorem:
Now let's say that the line \(\Vert F_2 \ F_1^*\Vert\) intersect at point \(B\) where \(B\) lies on the tangent line:
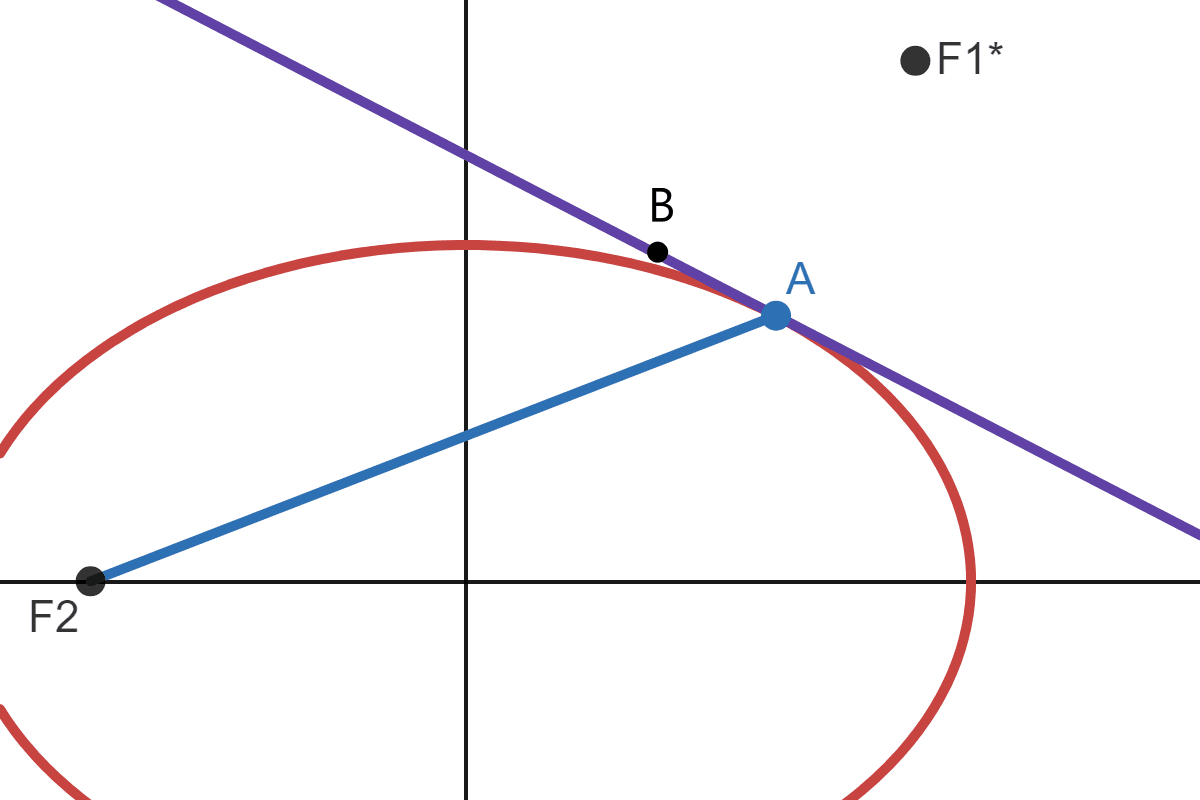
This means:
Since point \(F_1^*\) is a mirror image of \(F_1\), where the tangent line is the symmetric line, then all points on the tangent line is equidistant from \(F_1\) and \(F_1^*\):

This means point \(B\) is also equidistant from \(F_1\) and \(F_1^*\). Therefore:
This is our first claim. Now think about some random points inside and outside of the ellipse:
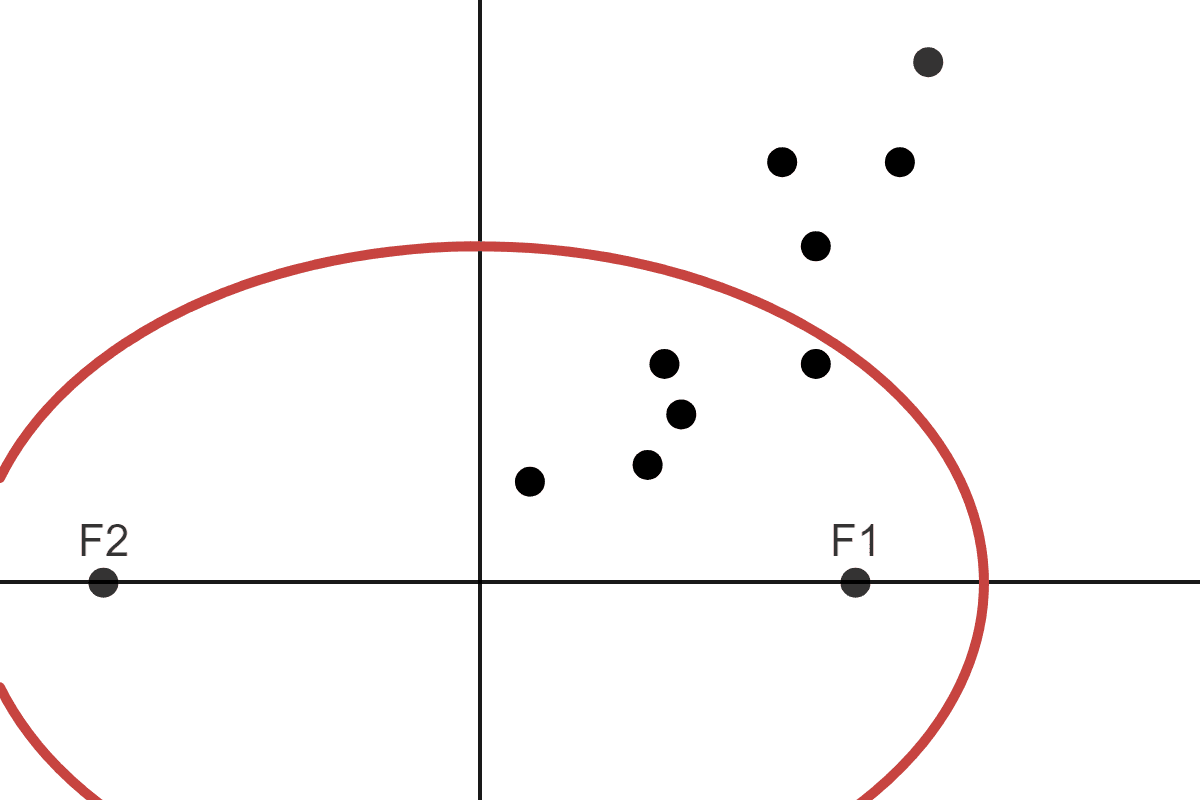
The ellipse is the locus of all points where the sum of the distances between a point and the two focii is always \(2a\). This means for a point inside the ellipse, the sum of the distances between that point and the two focii is always \(\lt 2a\). For a point outside the ellipse, the sum of the distances between that point and two focii is always \(\gt 2a\). Point \(B\) is a point outside the ellipse:

Since \(B\) is outside the ellipse:
This is our second claim, notice how it contradicts with the first claim. Since there is a contradiction, it cannot be possible that \(F_1^*\) does not lie on \(\scriptstyle{\overleftrightarrow{F_2 \ A}}\). Therefore, \(F_1^*\) definitely lies on the line \(\scriptstyle{\overleftrightarrow{F_2 \ A}}\), and this proves the reflective property of the ellipse.