Consider a circle with a random chord. Point \(B\) and \(C\) lies on the circumference and the chord:
Let \(O\) be the centre of the circle. Since \(B\) and \(C\) lie on the circumference, line \(\overline{OA}\) and \(\overline{OC}\) are both radii. It is trivial that if the distance from a point \(P\) to \(B\) and the distance from \(P\) to \(C\) are not equal, then \(P\) cannot be the centre. Let's consider all the points that are in the circle and are equidistant:
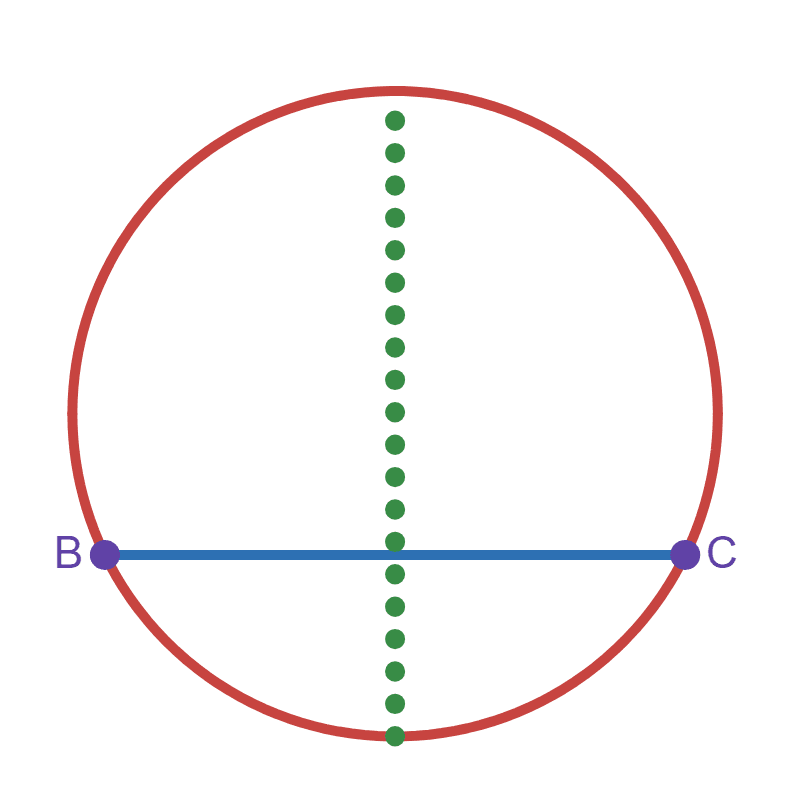
The locii of these point would form a line that is the perpendiculat bisector of the chord \(\overline{BC}\), this is because the line would be equidistant from \(B\) and \(C\), and the angle between the line and the chord would be 90°.
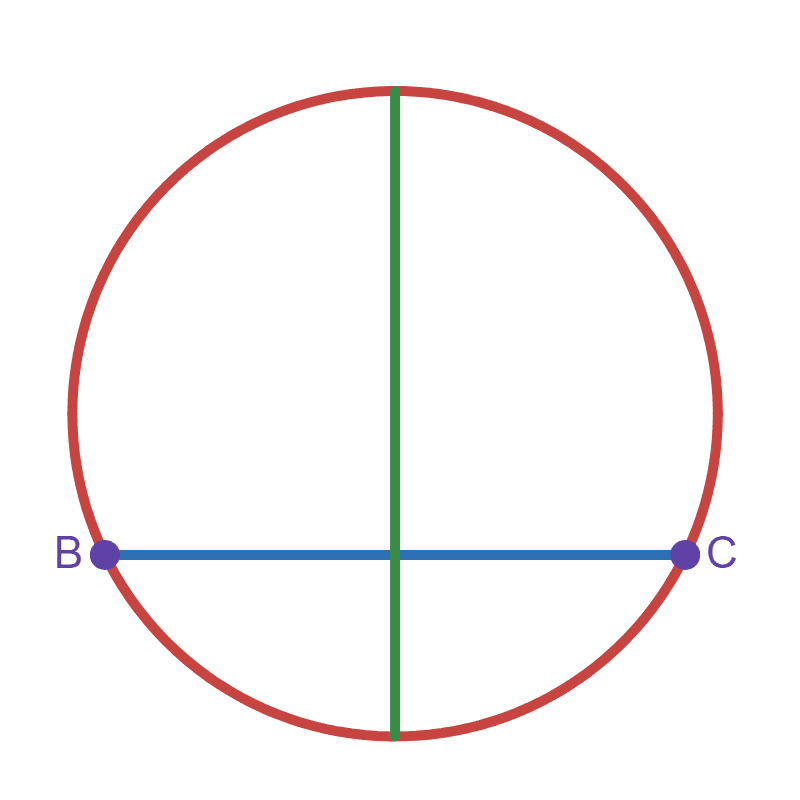
Since the centre of the circle is also equidistant from \(B\) and \(C\), the centre of the circle lies on this line. This means this line is actually a diametre. A similar argument can be made for any chord.