Proof of the inscribed angle theorem

Consider the circle:

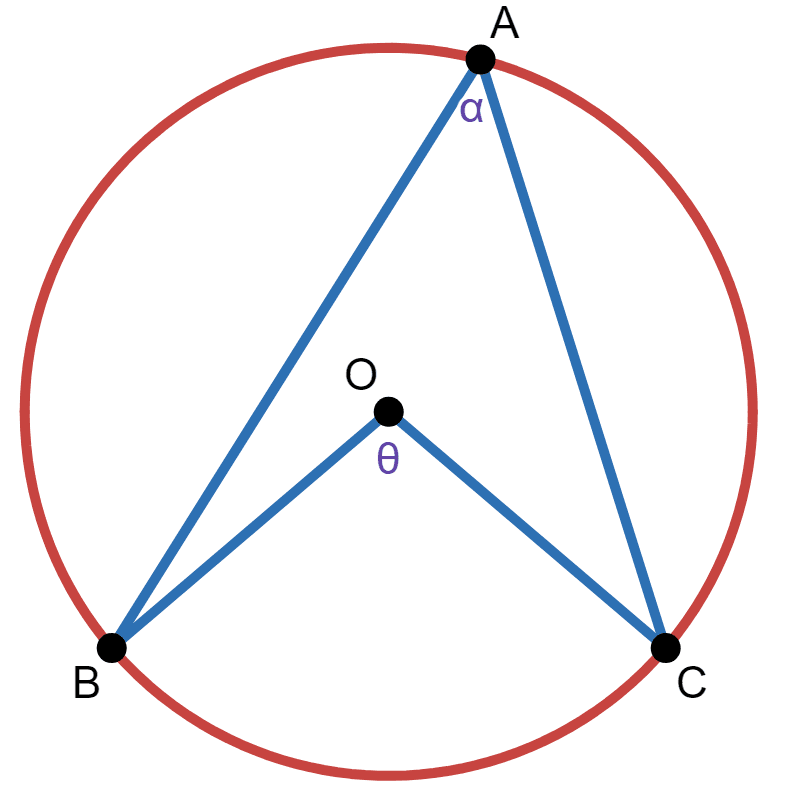
The angle \(BOC\) is \(\theta\) and the angle \(BAC\) is \(\alpha\). To prove the inscribed angle theorem, we will consider four cases: (1) when the center of the circle (point \(O\)) is inside the triangle \(ABC\); (2) when \(\overline{OA}\) is part of a diameter; (3) when point \(O\) is outside the triangle \(ABC\) but \(A\) still lies on the major arc \(BC\); (4) when point \(A\) lies on the minor arc \(BC\):

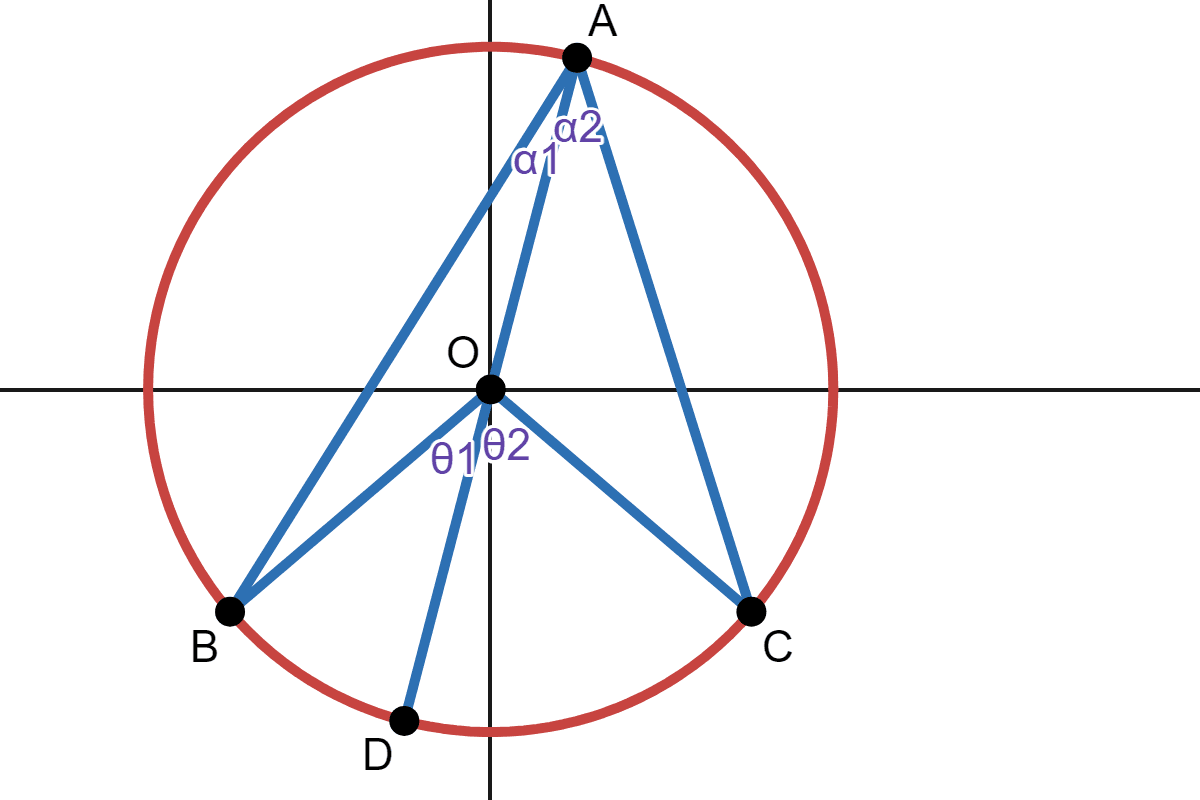
Let's focus on the first case for now. Let there be a diameter going through \(O\) and \(A\), and then touching another point called \(D\):

Let angle \(BOD\) be \(\theta_1\), angle \(DOC\) be \(\theta_2\), angle \(BAD\) be \(\alpha_1\) and angle \(DAC\) be \(\alpha_2\):

Since lines \(\overline{OA}\) and \(\overline{OC}\) are both radii, then angle \(OCA\) is also \(\alpha_2\). Let angle \(AOC\) be \(\epsilon_2\). Since angles in the triangle \(AOC\) add to 180:

\[\begin{gather} \epsilon_2 + 2\alpha_2 = 180 \\ 2 \alpha_2 = 180 - \epsilon_2 \end{gather} \]

Since \(\overline{OA}\) and \(\overline{OD}\) form a straight line:

\[\begin{gather} \theta_2 + \epsilon_2 = 180 \\ \theta_2 = 180 - \epsilon_2 \end{gather} \]

This shows that \(\theta_2 = 2 \alpha_2\). A similar argument can be made to show \(\theta_1 = 2 \alpha_1\). This means:

\[\begin{align} \theta_1 + \theta_2 &= 2 \alpha_1 + 2 \alpha_2 \\ &= 2 (\alpha_1 + \alpha_2) \\ \therefore \theta &= 2 \alpha \end{align} \]

This proves the inscribed angle theorem for the first case. During our proof, we showed that \(\theta_2 = 2 \alpha_2\), this fact proves the second case. Now let's consider the third case:

Let's draw a diameter going through point \(A\) and \(O\), and then touching the circle at point \(D\):

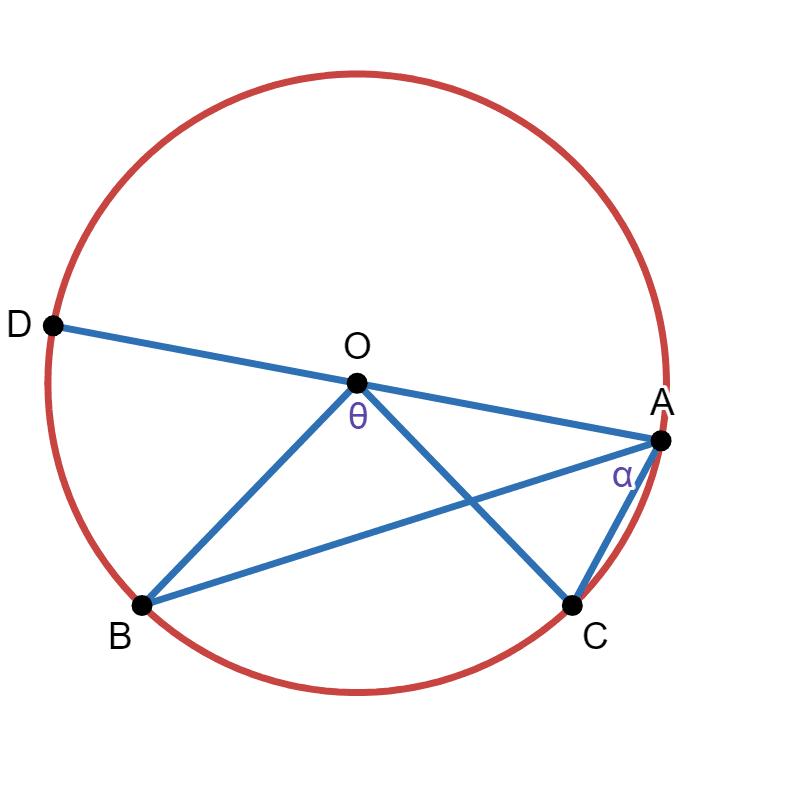
As proved earlier, angle \(BOD\) is double of angle \(BAD\). Let's call them \(\beta_1\) and \(\beta_2\) respectively. Similarly, angle \(COD\) is double of angle \(CAD\). Let's call them \(\epsilon_1\) and \(\epsilon_2\) respectively. This means:

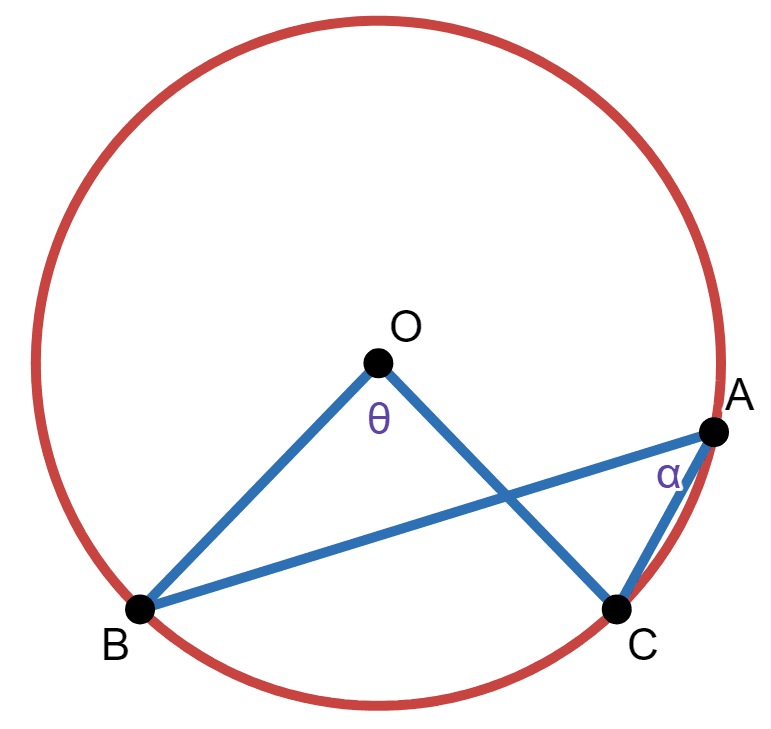
\[\begin{align} (\epsilon_1 = 2 \epsilon_2) ∧ (\beta_1 = 2 \beta_2) &\implies \epsilon_1 - \beta_1 = 2 (\epsilon_2 - \beta_2) \\ (\theta = \epsilon_1 - \beta_1) ∧ (\alpha = \epsilon_2 - \beta_2) &\implies \theta = 2 \alpha\end{align} \]

This proves the inscribed angle theorem for the third case. As for the fourth case, in can be confusing as to what angle is double of what angle:

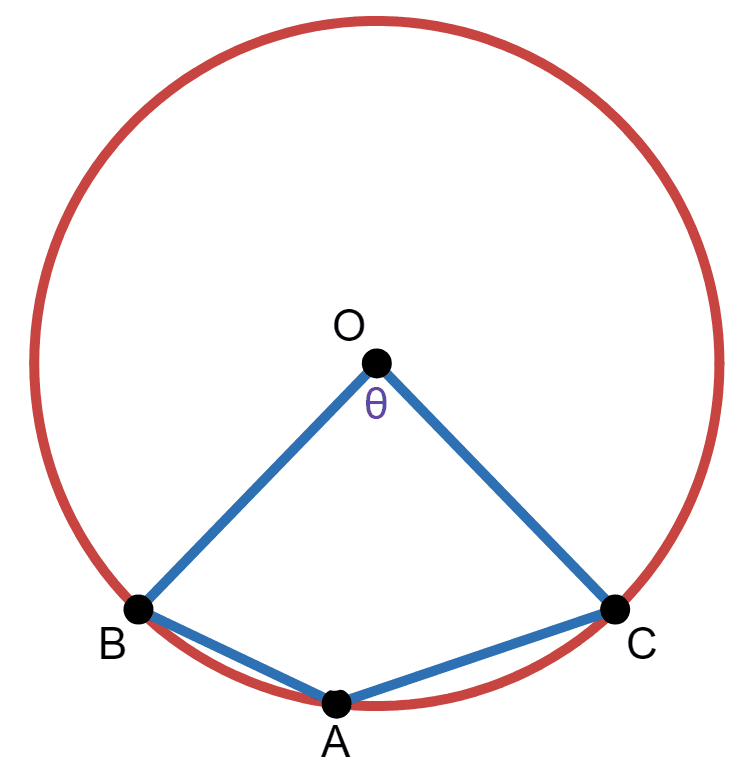
Let there be a diameter going through \(A\) and \(O\), and then touching the circle at point \(D\):

Let \(\beta\) be the angle \(BAC\), and let's say the diameter cuts \(\beta\) into \(\beta_1\) and \(\beta_2\). Let angle \(OAC\) be \(\beta_1\). Since lines \(\overline{OA}\) and \(\overline{OC}\) are both radii, then angle \(OCA\) be also \(\beta_1\). Similarly, angles \(OAB\) and \(OBA\) are both \(\beta_2\):

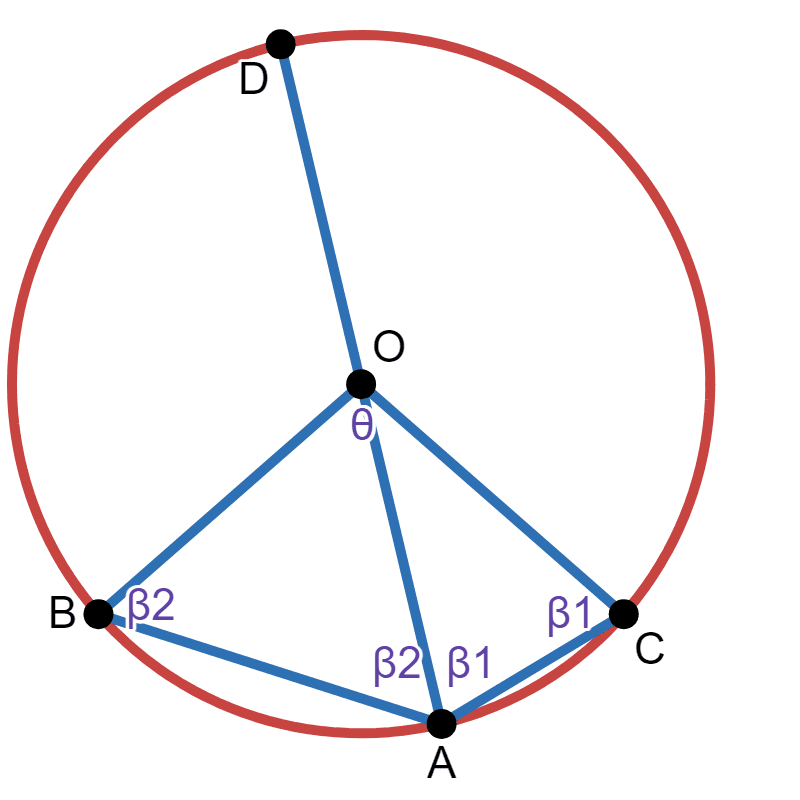
Similarly, let's say the diameter cuts \(\theta\) into \(\theta_1\) and \(\theta_2\):

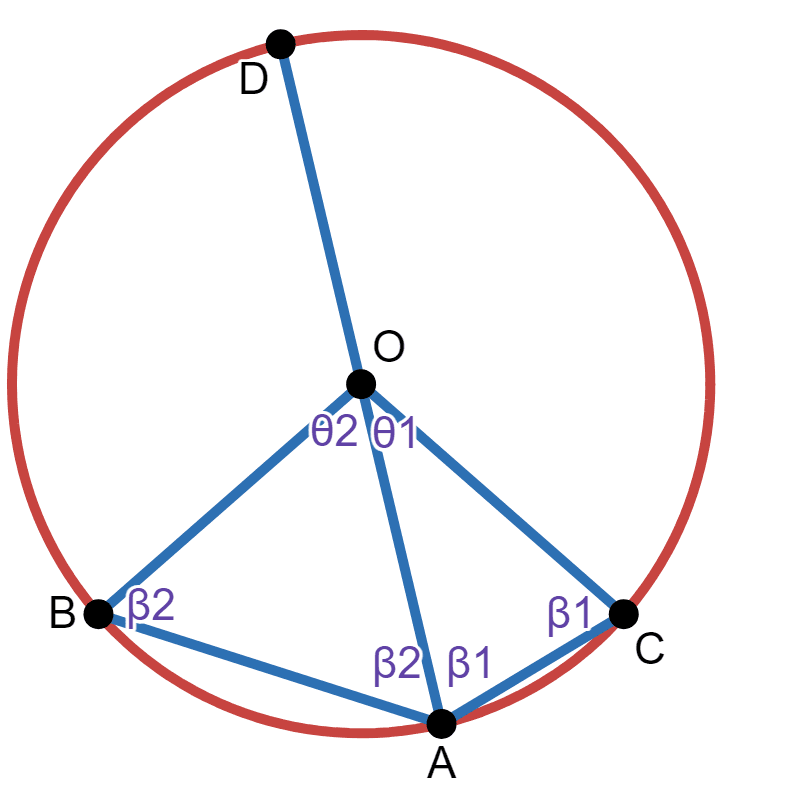
Since angles in a triangle add to 180:

\[\begin{gather} \theta_1 + 2\beta_1 = 180 \\ \theta_2 + 2\beta_2 = 180 \\ \theta_1 + \theta_2 + 2(\beta_1+\beta_2) = 360 \implies \theta + 2(\beta) = 360 \end{gather} \]

Let \(\epsilon\) be the larger angle at point \(O\):

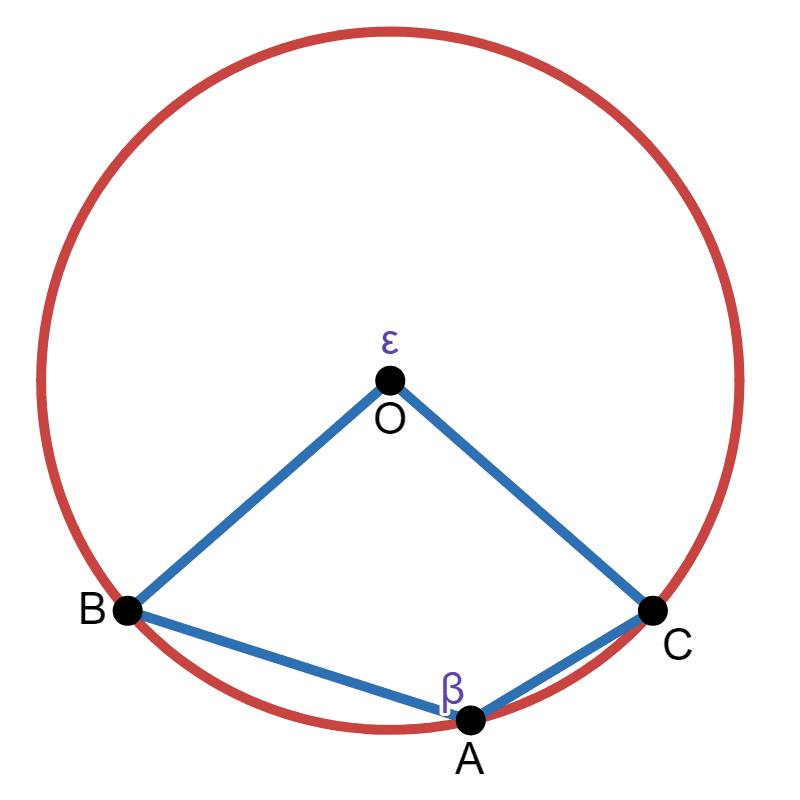
This means:

\[\begin{gather} 360 - \epsilon = \theta \\ \theta + 2 \beta = 360 \implies 360 - \epsilon + 2 \beta = 360 \\ \therefore 2 \beta = \epsilon \end{gather} \]

Proof Of The Inscribed Angle Theorem

Styles