We know that the equation for the sum of a geometric series is this:
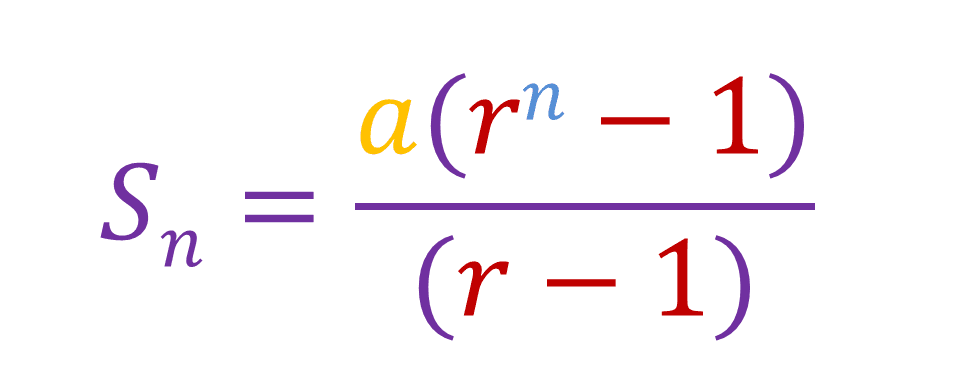
The first term is represented as a, the common ratio is r and Sn is the sum of a geometric sequence where n is the number of terms. Consider this series:
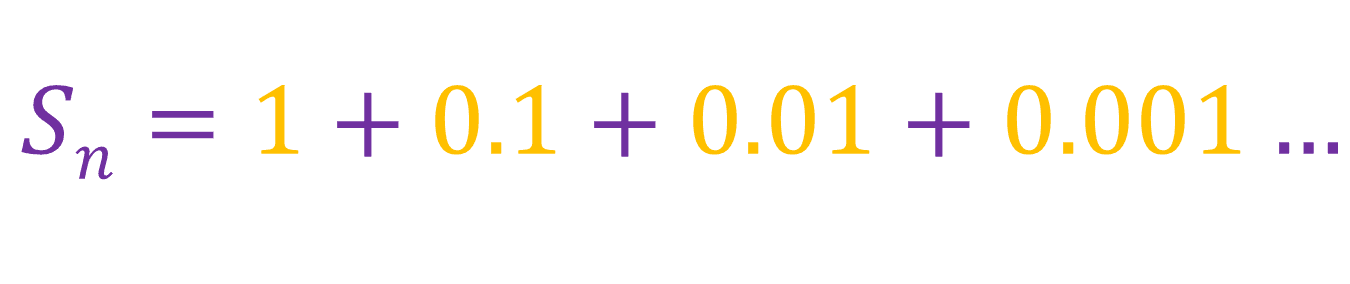
We know that r is 1/10, so:
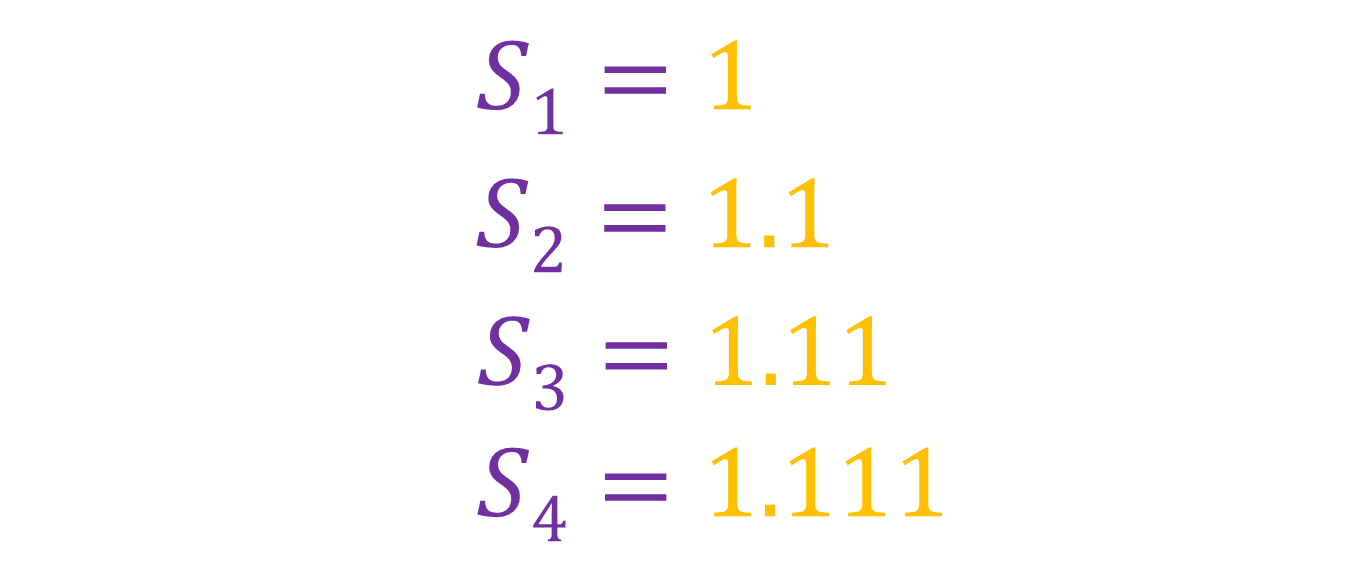
You can see that as n gets larger, the closer the sum gets to a limit, which means if we add infinity terms, we get:
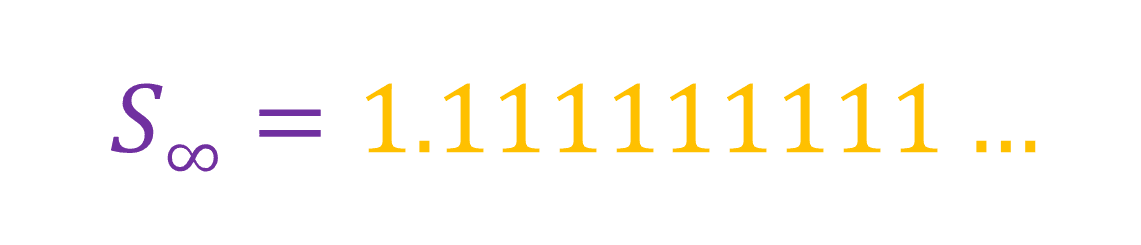
This is an example of a convergent series, because the more terms you add, the closer it gets to a particular limit (which in this case is 1.111...). A series is convergent only when r is less than one or more than minus one. Now suppose if n is infinity:
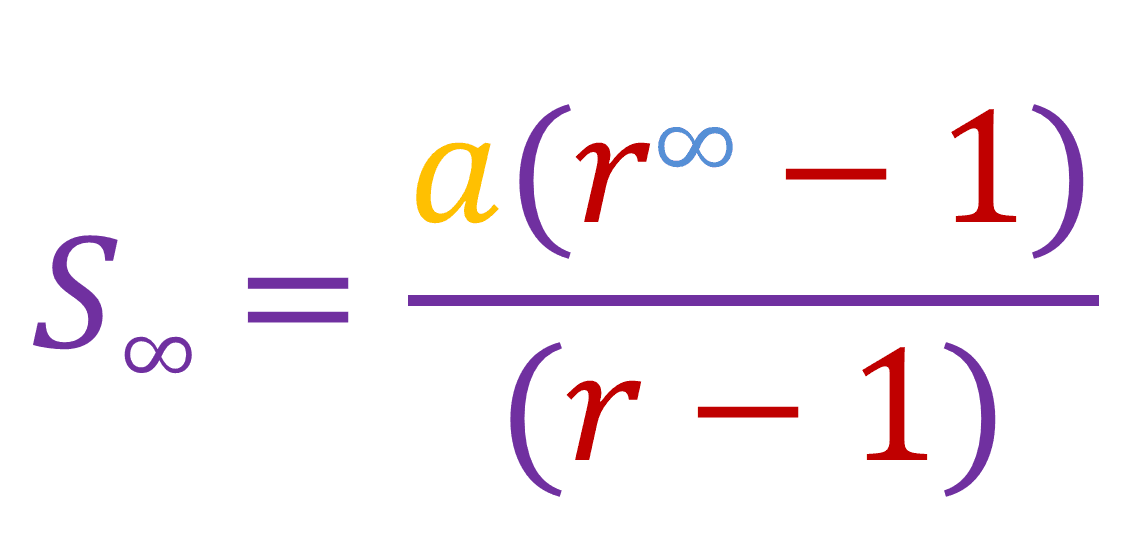
Since r is 0.something, then that means r∞ is equal to 0, therefore:

So now we get our equation, we can just multiply the numerator and denominator by -1 to get:
