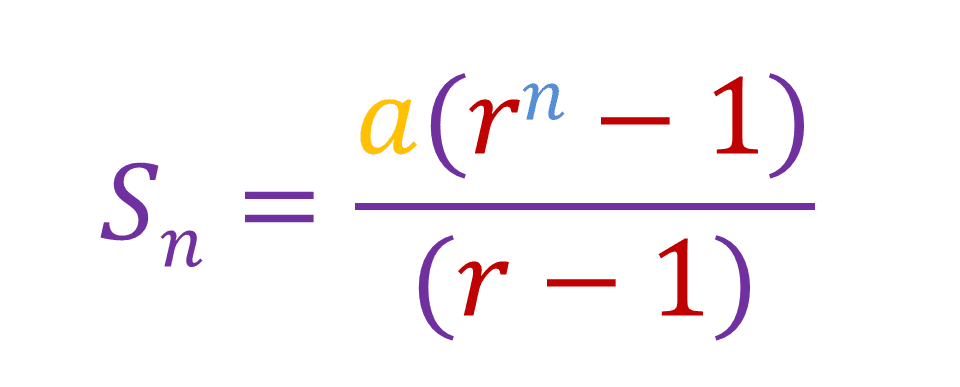We know that the sum of a geometric sequence would be like this:
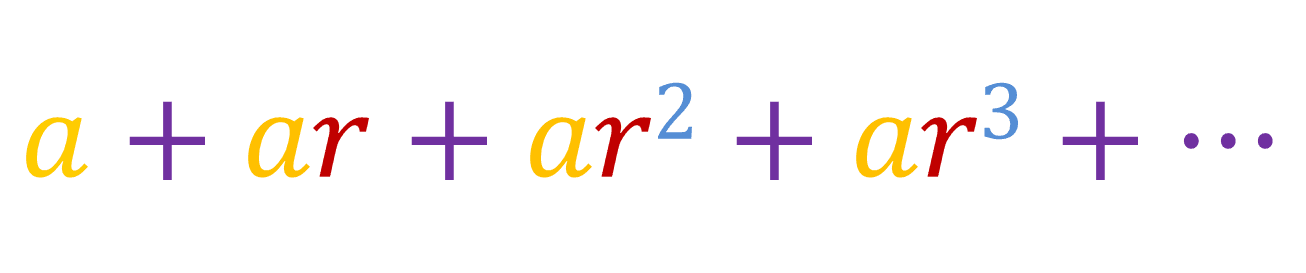
The first term is represented as a and the common ratio is r. Lets say Sn is equal to the sum of a geometric series where n is the number of terms:
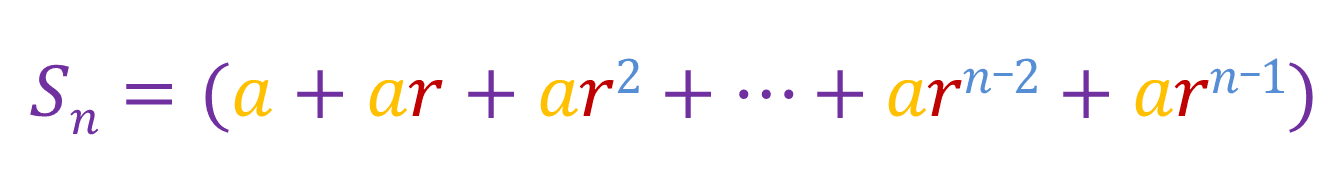
If we multiply both sides with r, we get:
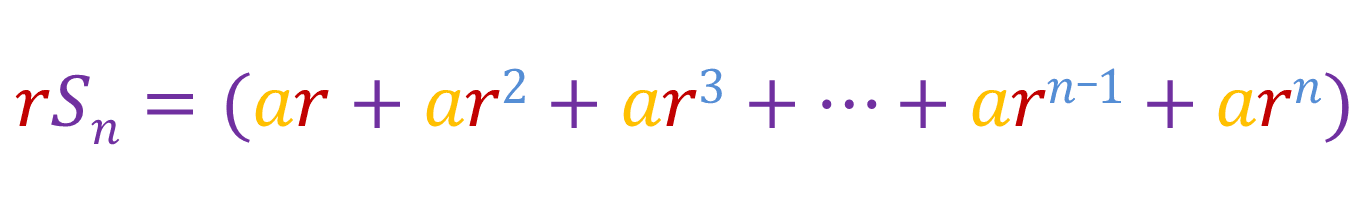
Now lets do [rSn - Sn]:
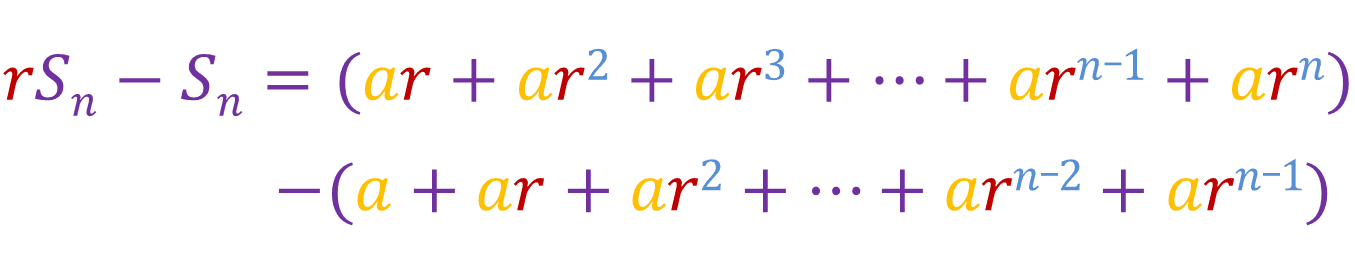
Now we can take Sn out and cancel out the like terms:
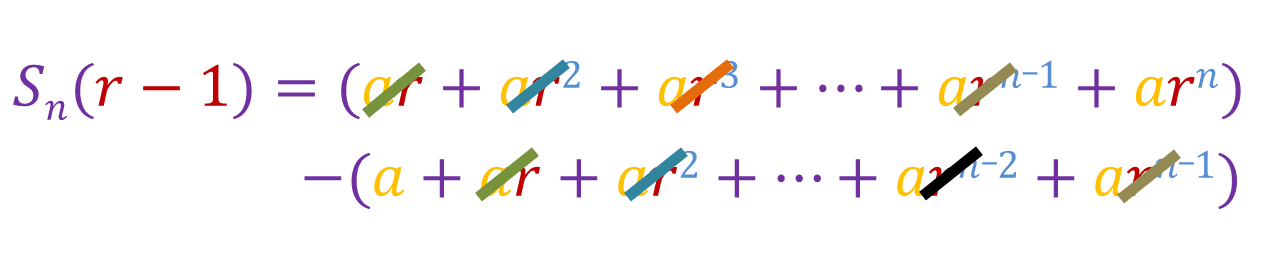
Now simplify:
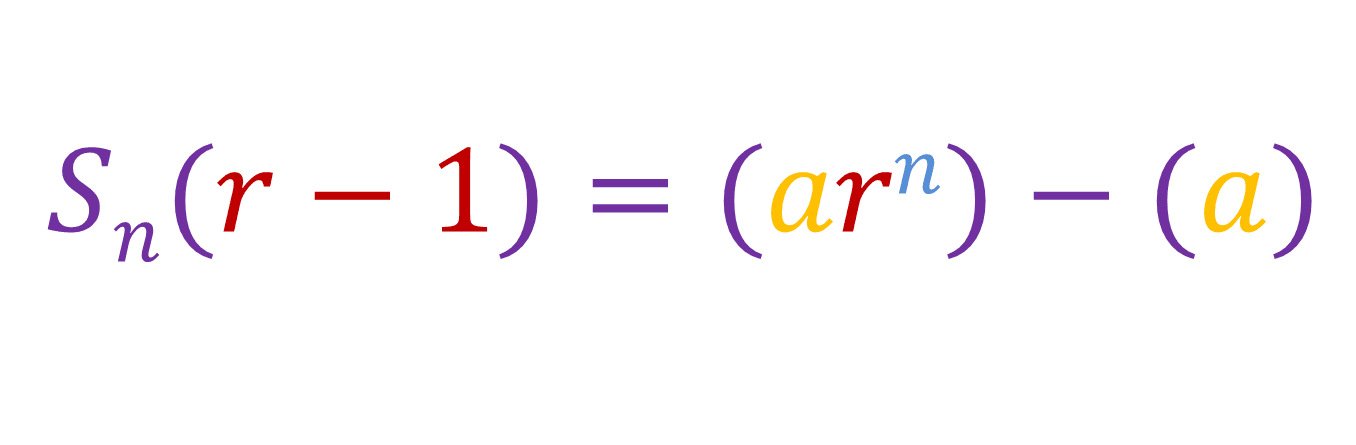
Now we just factor out the a:
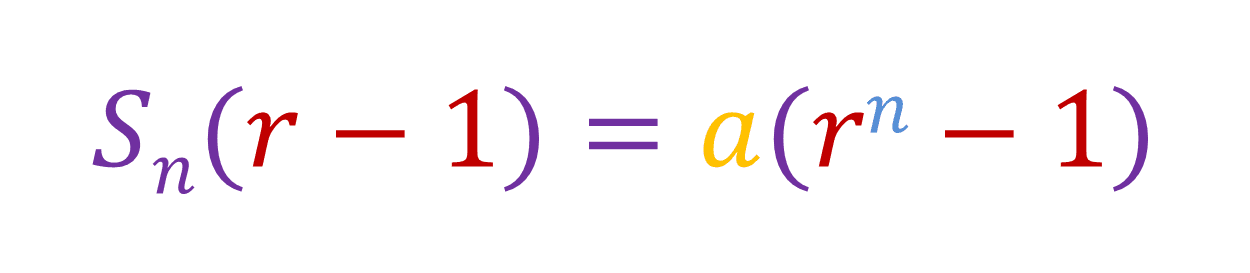
Now if we bring [r - 1] to the left hand side, we get our equation: