The table below represents Pascal's triangle:
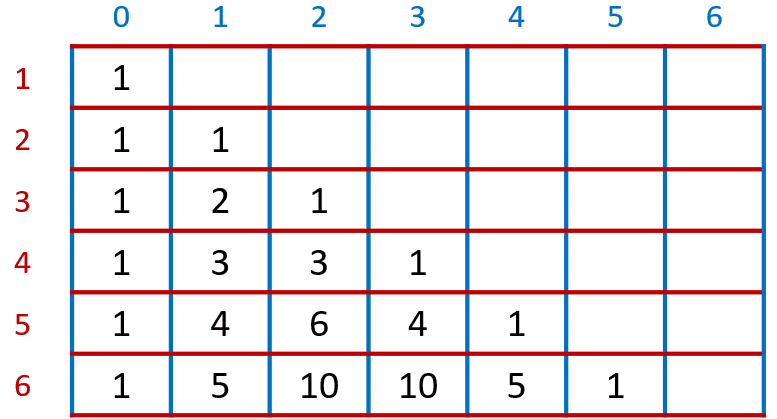
Lets use variable r to represent the row (which starts from 1) and variable c to represent the column (which starts from 0). In row 4 and column 2, you will see the number 3, and in column 3, you will see 1, and if you add the two numbers, you get 4. Since this is the Pascal's triangle, it makes sense that [(the number in position r and c - 1) + (the number in position r and c) = (the number in position r + 1 and c)], but how about using combinations to represent the numbers in Pascal's triangle, like this:
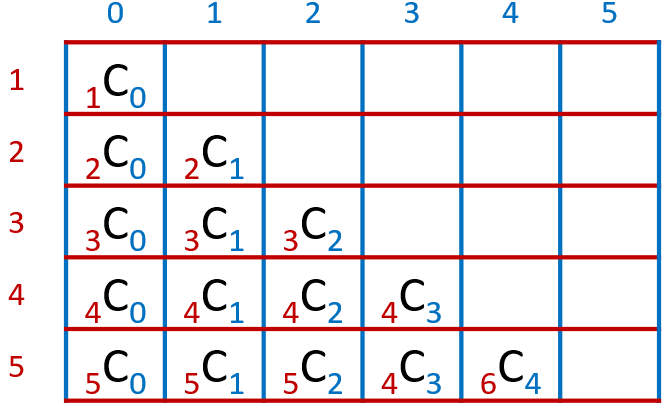
It's easier to find a number in the Pascal's triangle using [rCc], where r is the row and c is the column. You can use a calculator to check if this holds true for the first few rows, but how do we know that this works for all the rows in Pascal's triangle? In other words, what if there is a specific row for which [rCc] doesn't work?
No matter which row we choose, [rC0] will always be 1, and since the first number in every row of the Pascal's triangle is 1, then we know that [rCc] holds true for the first number in every row. Now what about all the other numbers? For that, we would have to prove that [rCc-1 + rCc = r+1Cc]. To do this, start by expanding and simplifying [rCc-1 + rCc]:
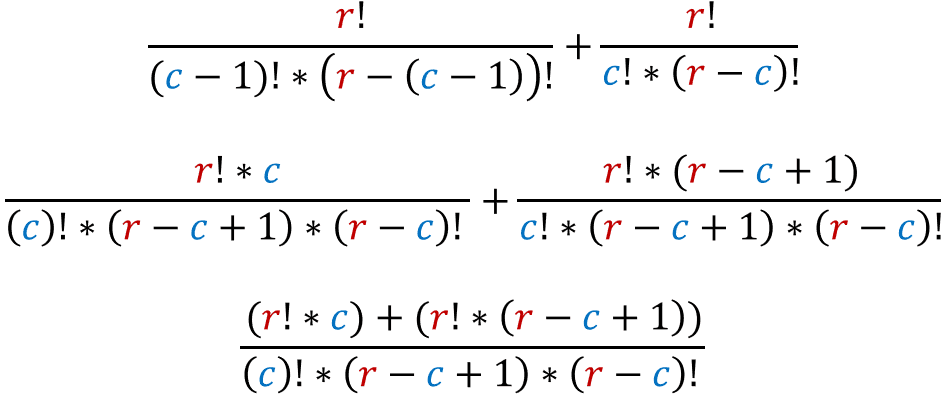
If we simplify this even further:
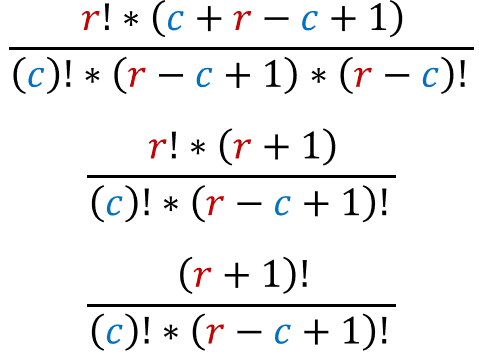
And this is [r+1Cc].
Since we already know that [rCc] works for the first few rows, then by using the equation [rCc-1 + rCc = r+1Cc], we know that [rCc] will work for other rows as well.