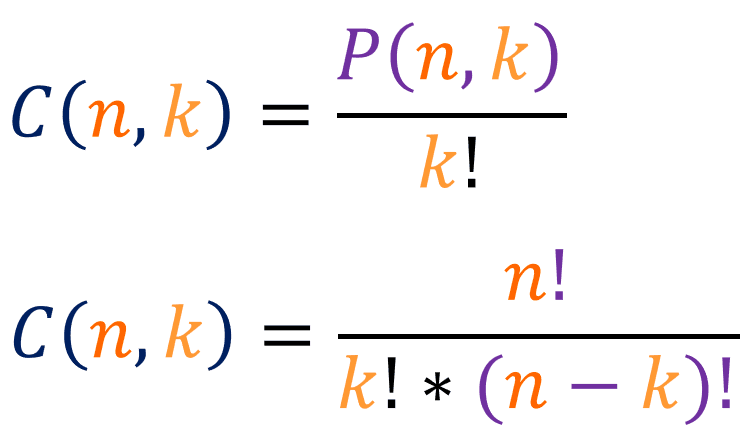Suppose out of these four letters I want to arrange three of them:
Using permutations, we know that there are P(4,3) (= 24) ways to do it:
Each arrangement like [A, B, C] or [B, A, C] is a different permutations, but what if order didn't matter? What if we didn't care whether its [A, B, C] or [B, A ,C]? This is where combinations come in. Combinations tell you how many unique arrangements you can have, by unique I mean the letters in each arrangement cannot be the same. For example [A, B, C] and [D, A , B] are two different combinations, but [A, B, C] and [C, B, A] are the same in terms of combinations. In our previous example, there is only 4 combinations:
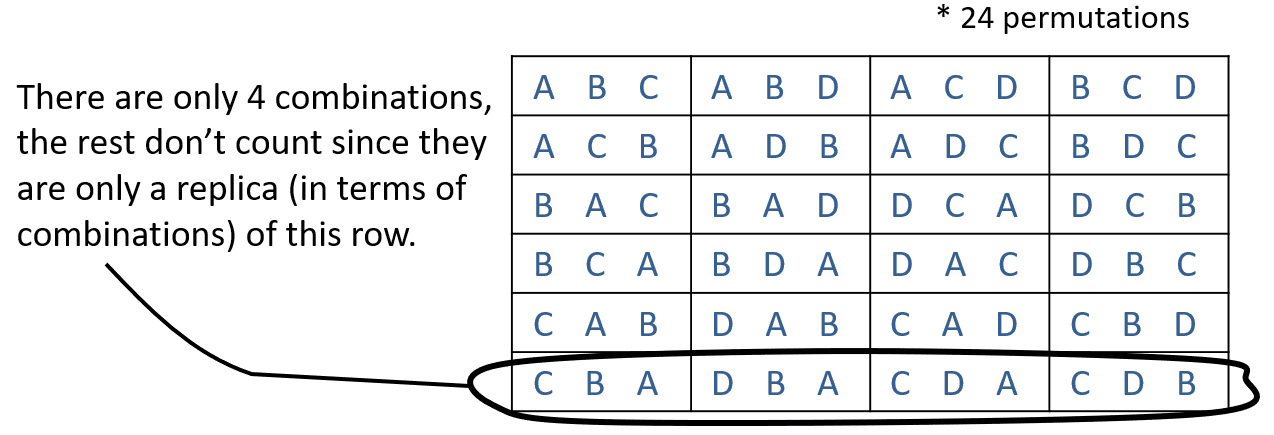
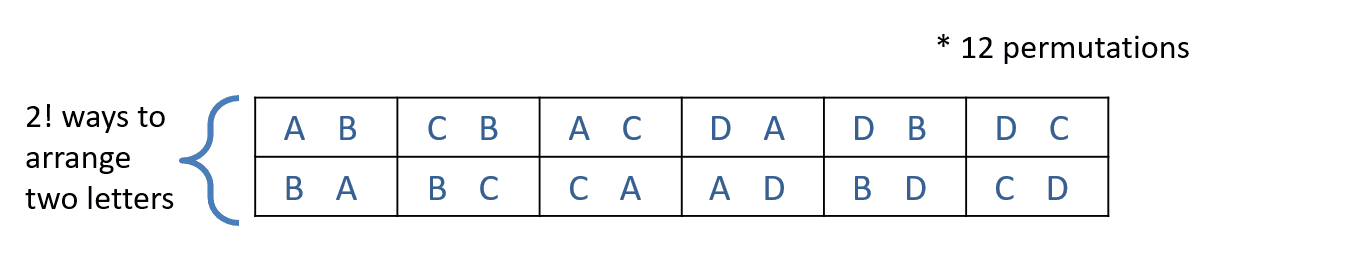
There are 3! ways of arranging three letters, and if you look at the above table closely, you will notice that the reason it has 6 rows is because 3! = 6. For example, in the last row, [C, B, A] is one of the arrangements, but since there are 3! ways of arranging [C, B, A], you would need 6 rows to present all of those arrangements, the same goes for [D, B, A], [C, D, A] and [C, D, B]. The notation of permutations is this [P(n,k)] and this [nPk]. Similarly for combinations, the notation is like this [C(n,k)] and this [nCk]. Now using the above letters, lets try to find 4C2:
Out of four letters, if we want to arrange them in groups of twos, then there are (4C2 =) 6 ways to do it (provided that the order doesn't matter). Since there are 2! ways to arrange two letters, then that must mean [4P2 = 4C2 * 2!]:
Using the above examples, we can deduce that [nCk * k! = nPk], because [(the number of groups with unique elements) * (number of ways you can arrange the elements in one group) = (number of groups where each group has a different arrangement whether the elements are repeated to not)]. To understand this better, you should use your own examples. We can also use the above statement to derive the formula for combinations:
