The function tan(x) can be written as sin(x)/cos(x), therefore:
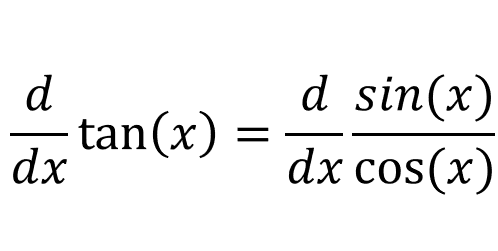
If we use the qoutient rule:
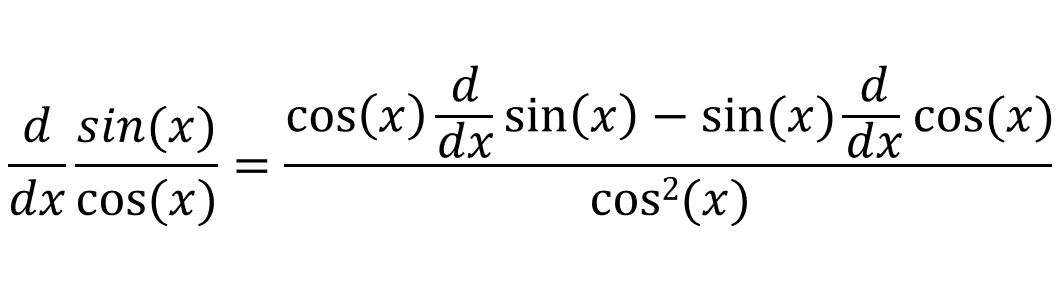
If we simplify this:
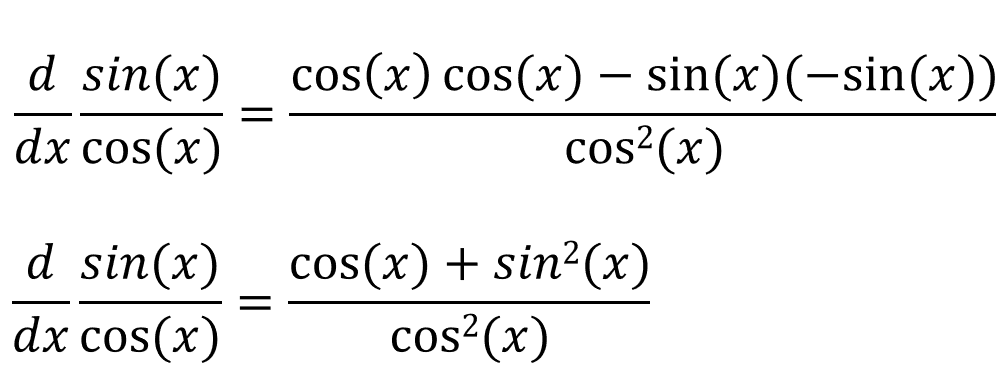
If we simplify this further:
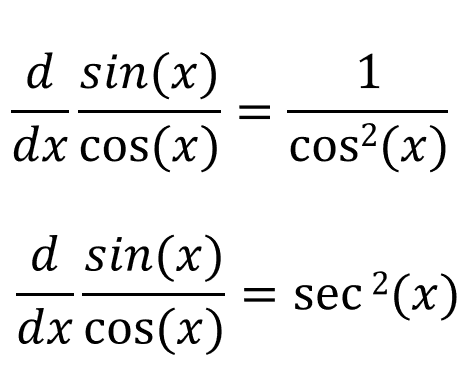
So the derivative of tan(x) is sec2(x).
The function tan(x) can be written as sin(x)/cos(x), therefore:
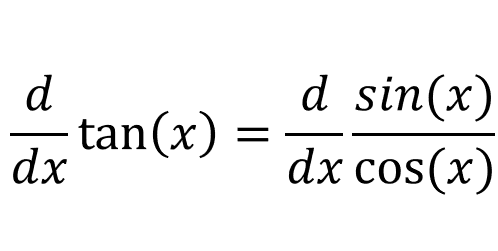
If we use the qoutient rule:
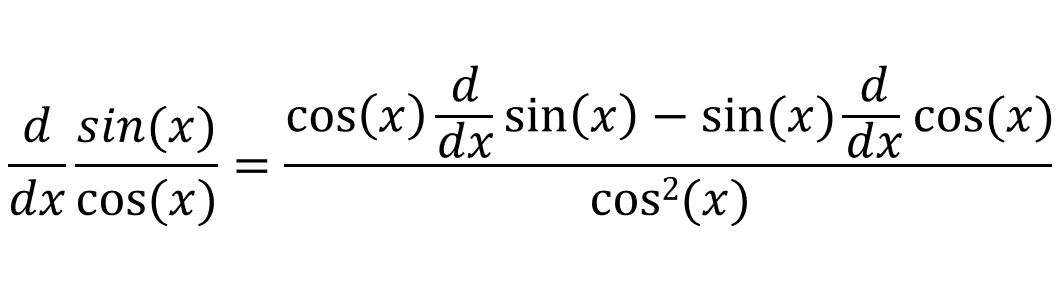
If we simplify this:
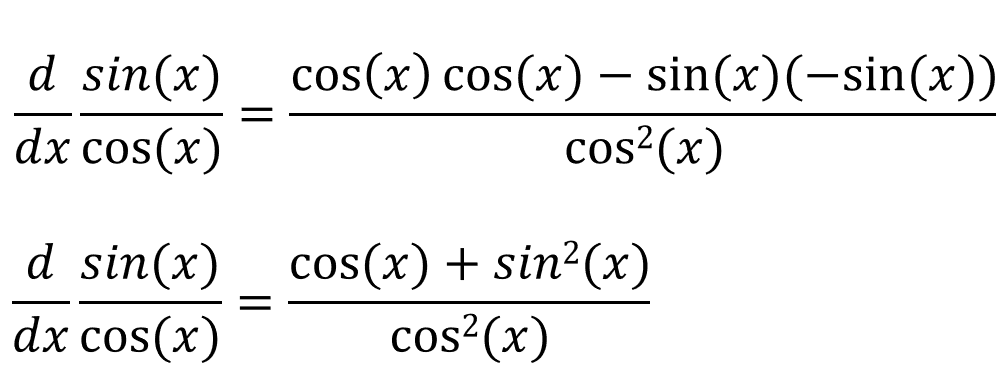
If we simplify this further:
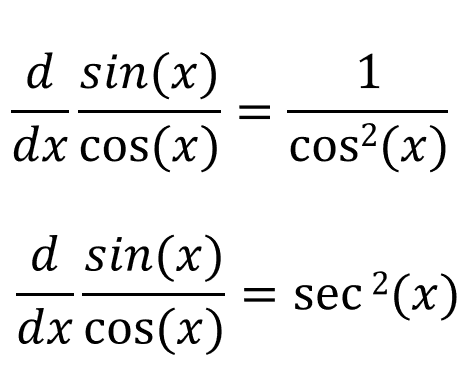
So the derivative of tan(x) is sec2(x).