We can write sec(x) in terms of cos(x):
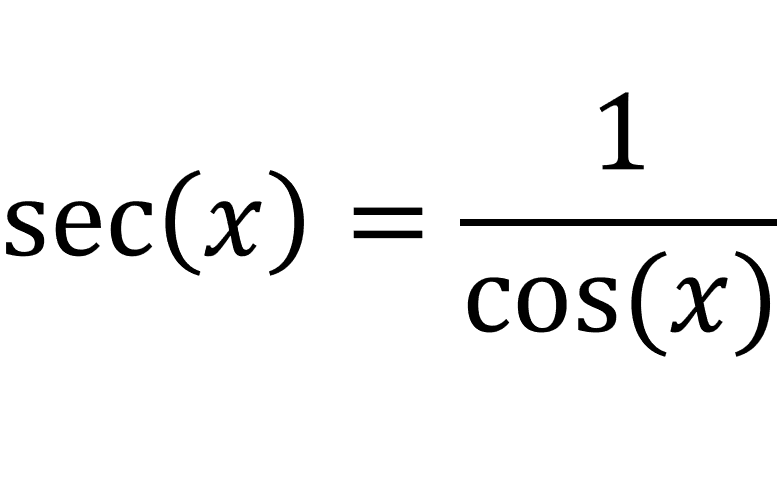
So differentiating sec(x) would just mean to differentiate 1/cos(x):
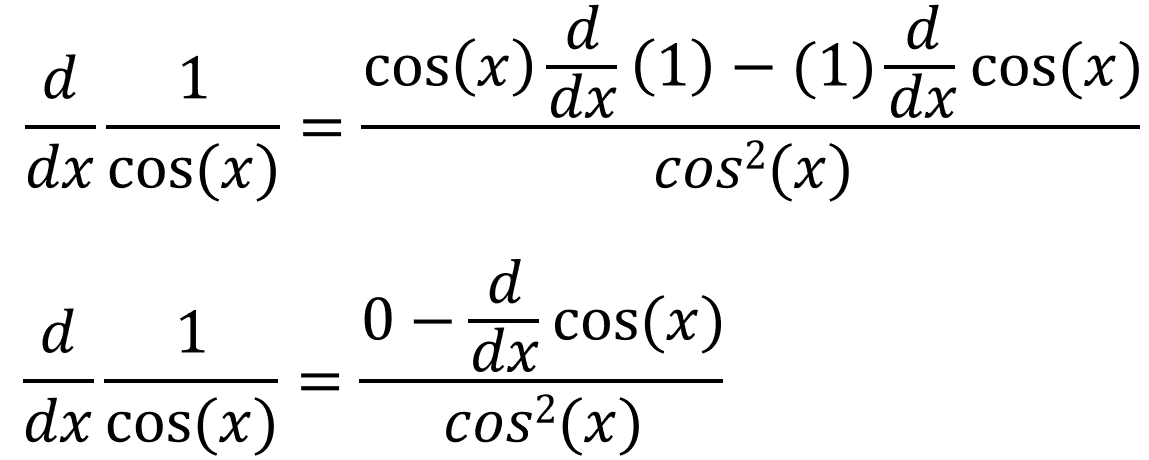
If we simplify this further:
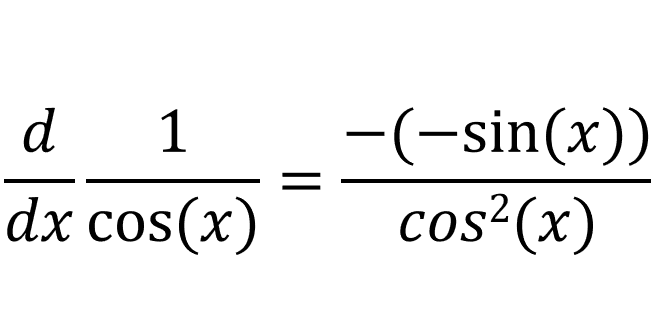
We know that tan(x) = sin(x)/cos(x), so:
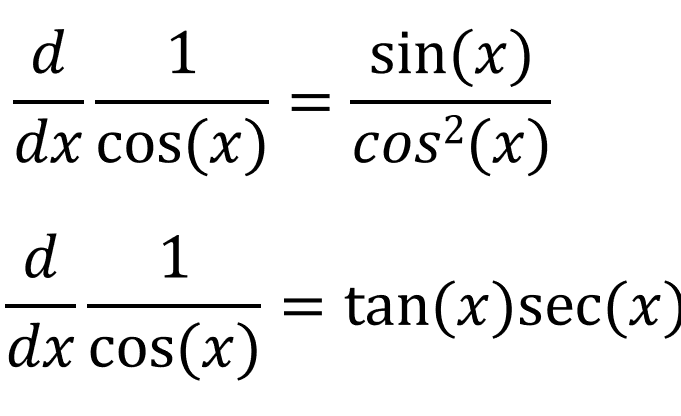
So the derivative of sec(x) is sec(x)tan(x).
We can write sec(x) in terms of cos(x):
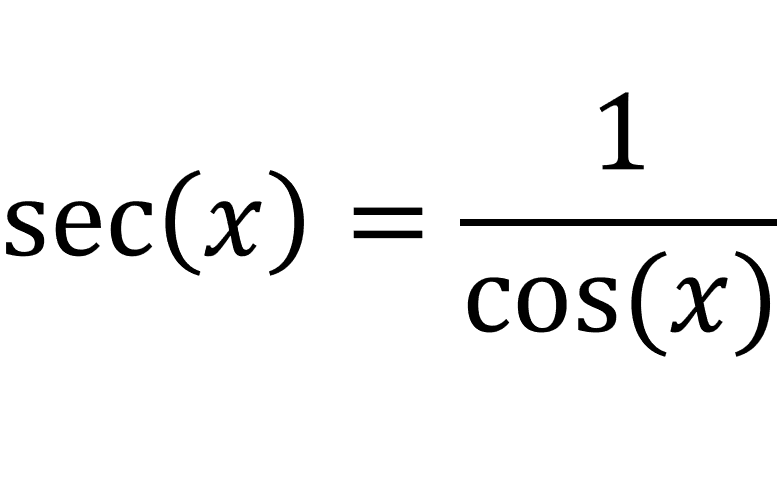
So differentiating sec(x) would just mean to differentiate 1/cos(x):
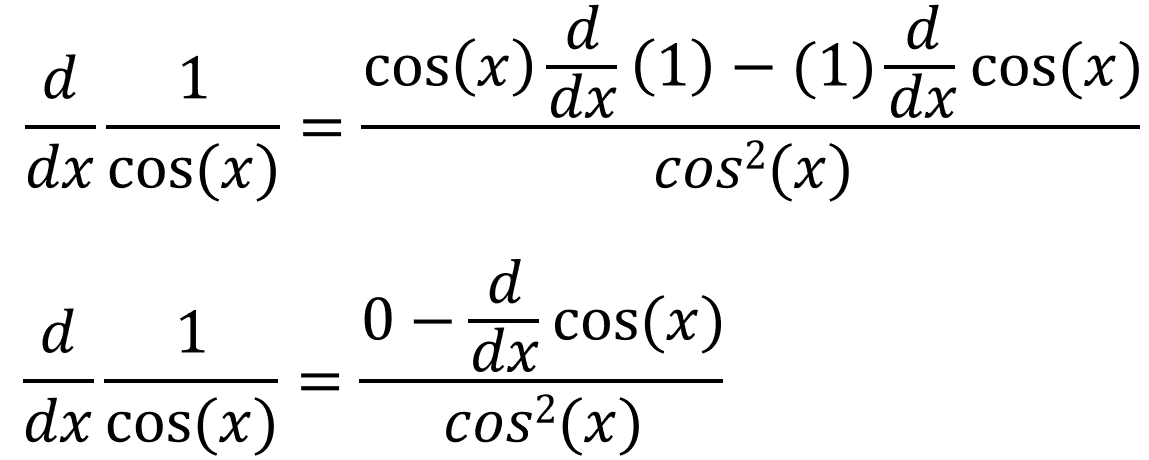
If we simplify this further:
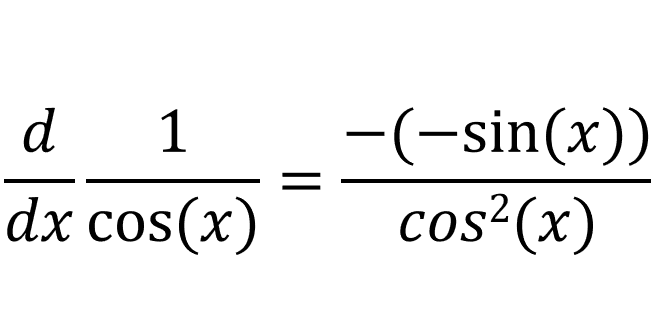
We know that tan(x) = sin(x)/cos(x), so:
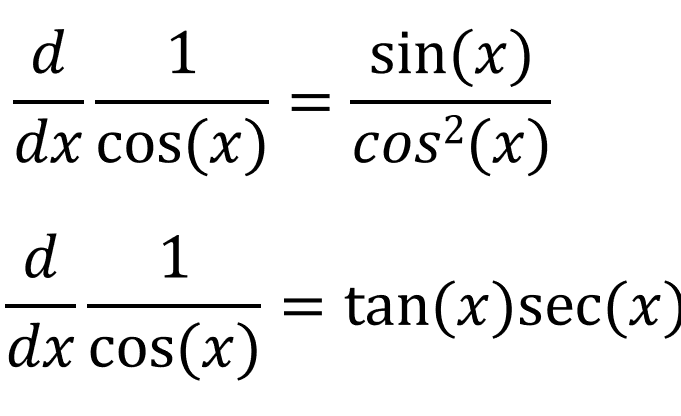
So the derivative of sec(x) is sec(x)tan(x).