Proof Of The Derivative Of arcsin(x)

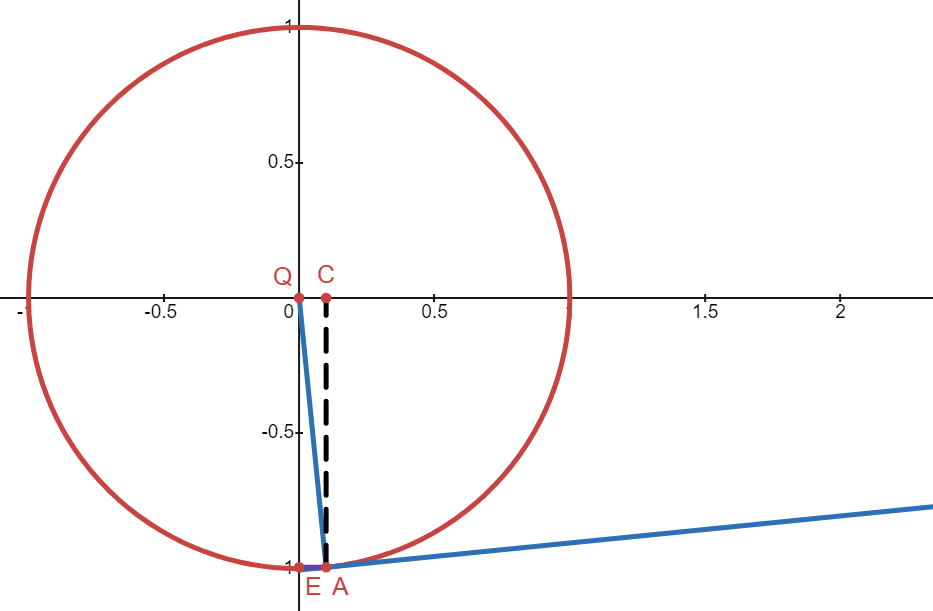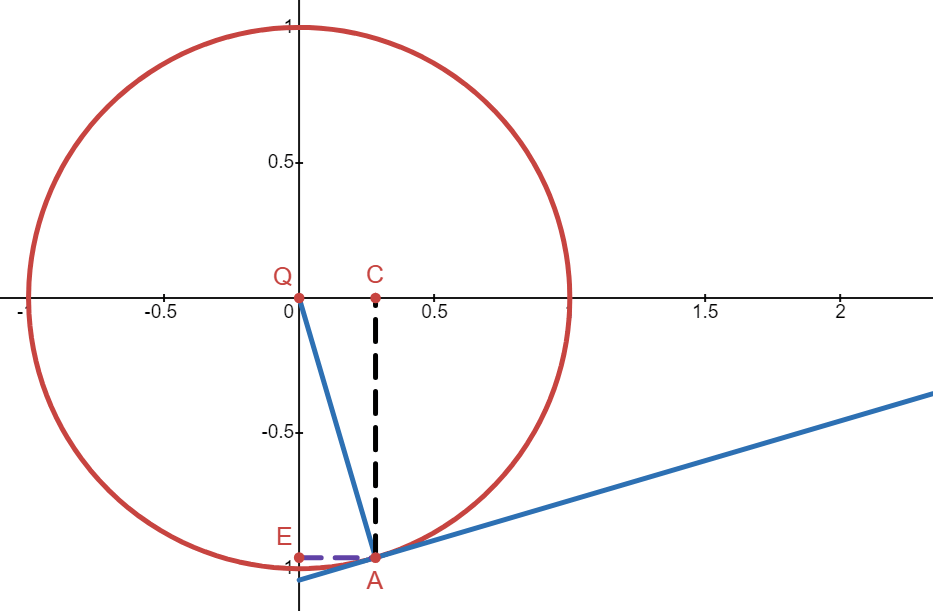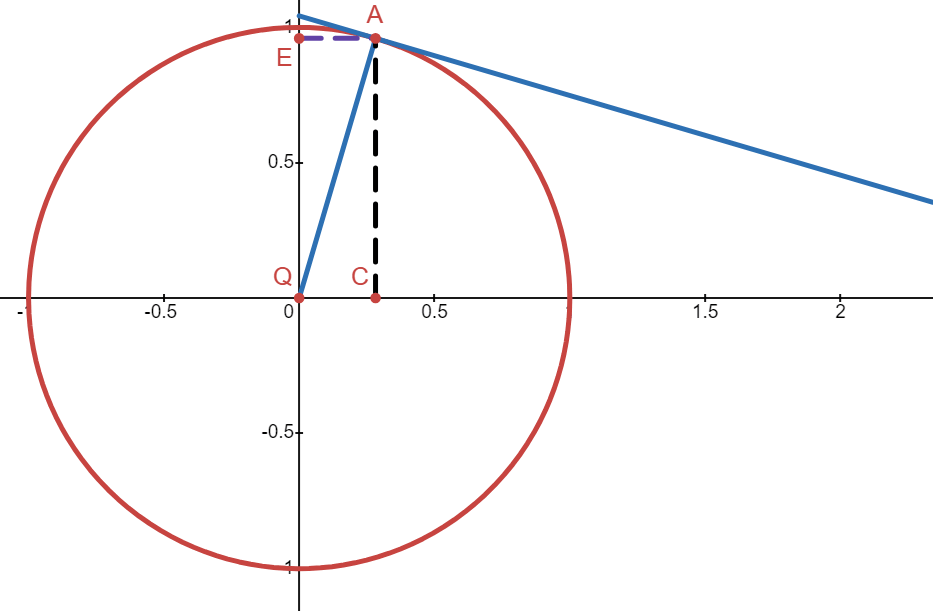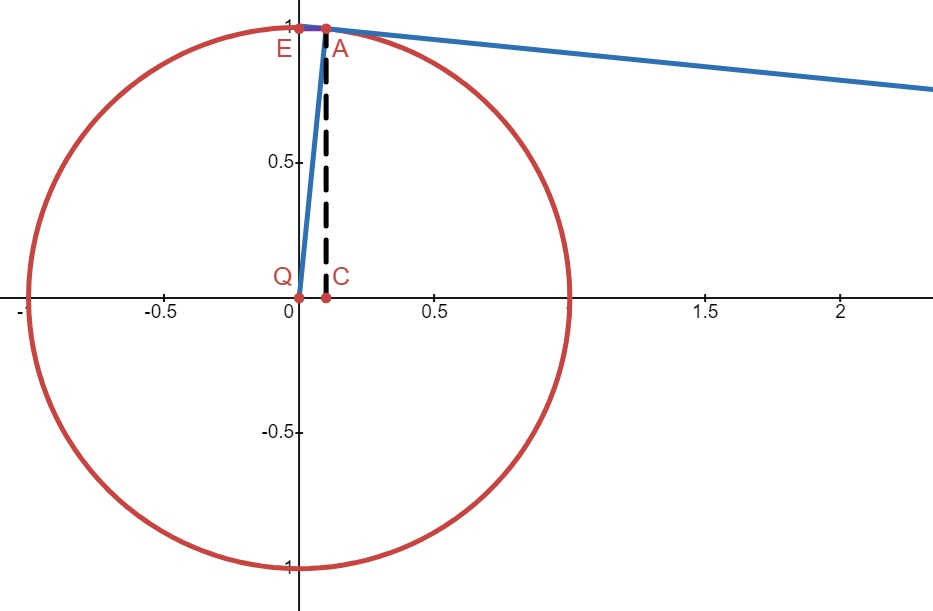
First look at this unit circle:

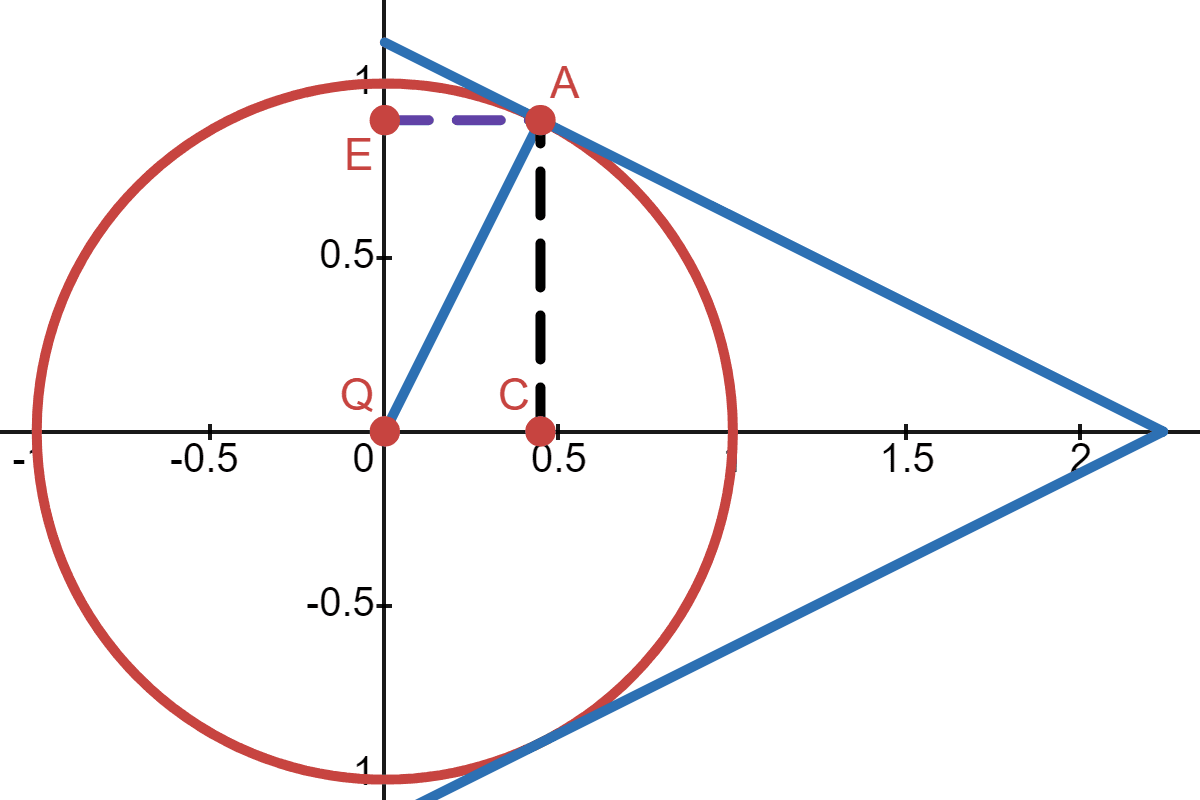
Let \(y\) be the angle between the line \(\overline{QA}\) and the x-axis. Let \(x\) be the signed distance from \(C\) to \(A\). This means \(x = \sin(y)\), and:

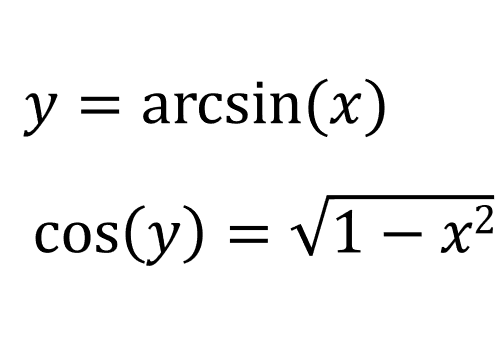
We want to find the derivative to \(y = \arcsin(x)\). The domain is \([-1,1]\), and the range is \(y \in [\frac{-\pi}{2} , \frac{\pi}{2}]\):

This means \(\cos(y)\) will always be a positive value. We already know that the derivative of x with respect to x is 1:

Since \(x = \sin(y)\):

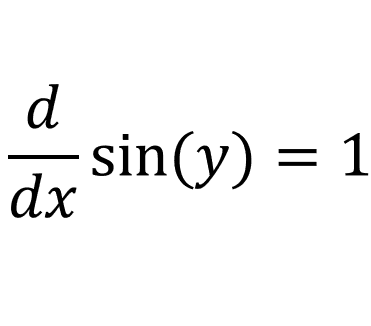
Using the chain rule:

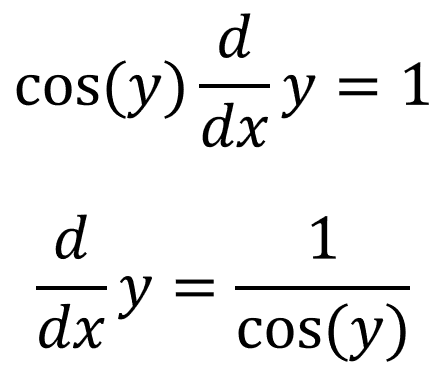
And we already know what \(\cos(y)\) is:

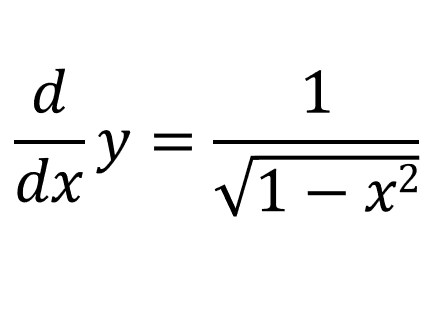
Keep in mind that \(\cos(y)\) will always be positive since \(y \in [\frac{-\pi}{2} , \frac{\pi}{2}]\), so \(\sqrt{1-x^2}\) will also always be positive. Now let's find the derivative of \(\arcsin(\frac{x}{a})\). We can use the chain rule:

\[\frac{d}{dx} \arcsin \left( \frac{x}{a} \right) = \frac{1}{\sqrt{1-\frac{x^2}{a^2}}} \frac{1}{a}\]

Since \(\cos(y)\) is always positive, so:

\[\frac{d}{dx} \arcsin \left( \frac{x}{a} \right) = \frac{1}{\left| \sqrt{1-\frac{x^2}{a^2}} \right|} \frac{1}{a}\]

We can put \(a\) inside the square root as well:

\[\frac{d}{dx} \arcsin \left(\frac{x}{a} \right) = \frac{1}{\left| \sqrt{1-\frac{x^2}{a^2}} \right|} \frac{\operatorname{sign}(a)}{|a|} = \frac{\operatorname{sign}(a)}{| \sqrt{a^2-x^2} |}\]