Below is a graph of arccosecant(x). The range of this function is \([\pi/2, 0) \cup (0,-\pi/2]\):
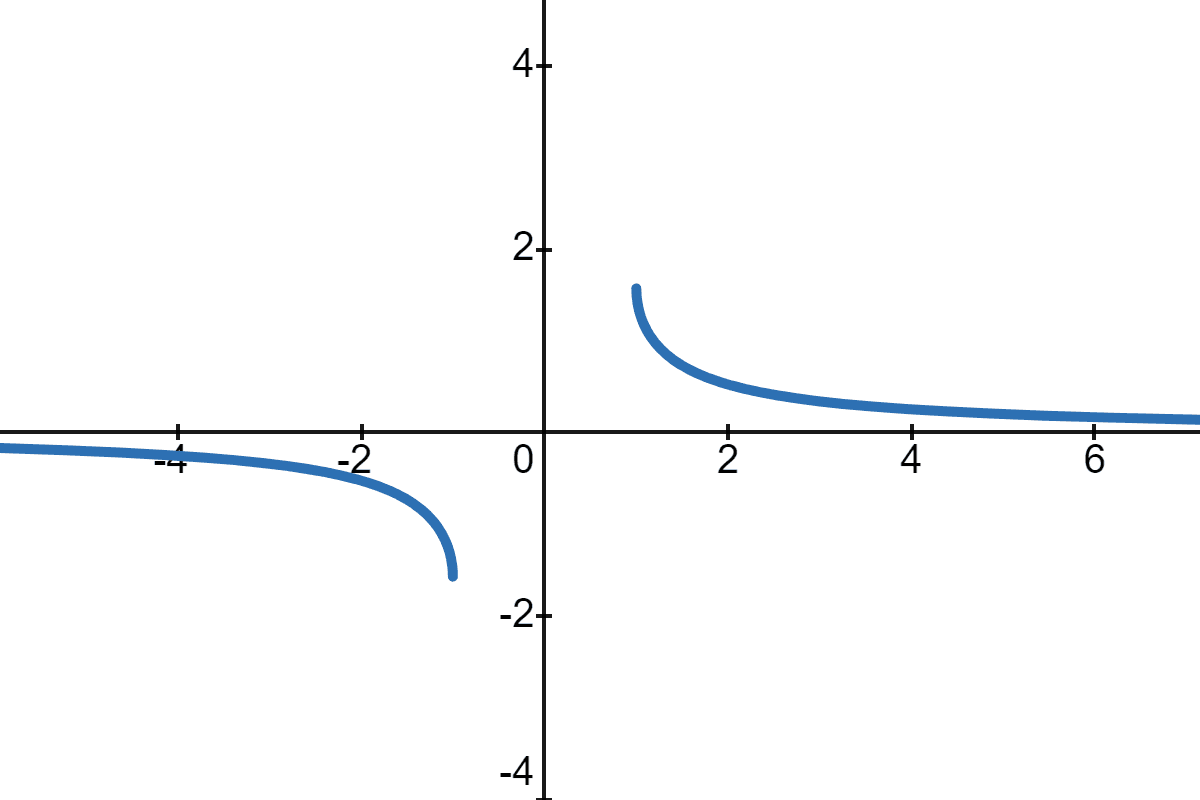
Look at this unit circle:
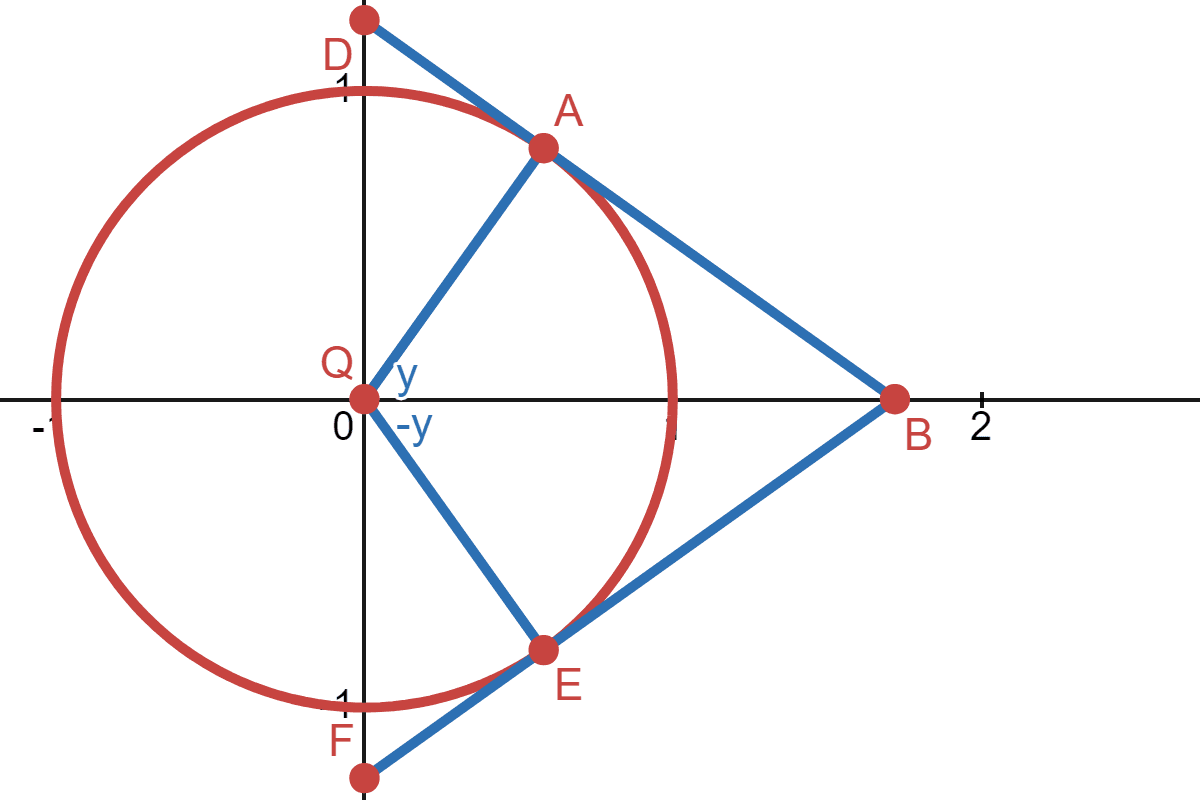
Let \(x\) be the distance from point \(Q\) to \(D\), and let \(y\) be the angle between the line \(\overline{QA}\) and the x-axis. This means cosec(y) is the distance from point \(Q\) to \(D\), and cosec(-y) is the negative distance from point \(Q\) to \(F\). If arccosec(x) = y:
\[ \begin{align} \operatorname{cosec}(y) &= x \\ \cot(y) &= ±\sqrt{x^2 - 1} \end{align}\]
The cotagent would be negative if x is negative:
\[ \cot(y) = \frac{|x|}{x} \left| \sqrt{x^2 - 1} \right| \]
As for the derivative of arccosec, let's start with:

Since x = cosec(y):
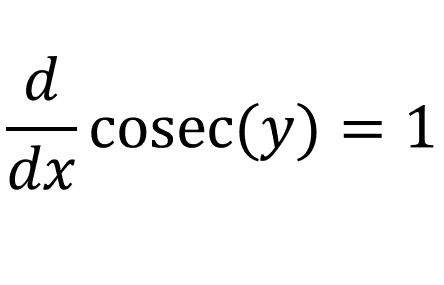
Using the chain rule:
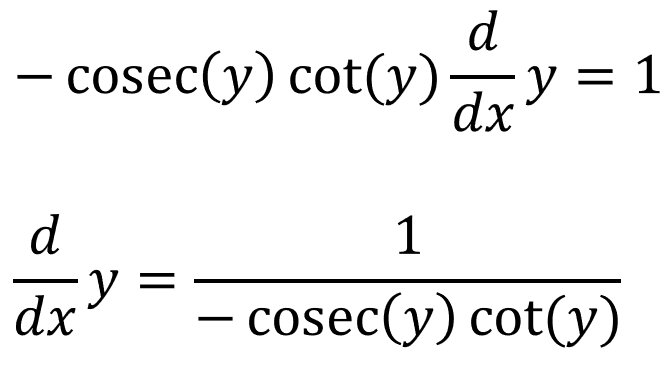
And we already know what cosec(y) and cotan(y) is equal to:
\[\frac{d}{dx}y = - \frac{1}{x \frac{|x|}{x} \left| \sqrt{x^2 - 1} \right|} = - \frac{1}{ |x| \left| \sqrt{x^2 - 1} \right|}\]
Below is the graph of the derivative (green):
