Below is a unit circle where the angle (\(y\)) changes from \(\approx \pi\) to \(\approx 0\):
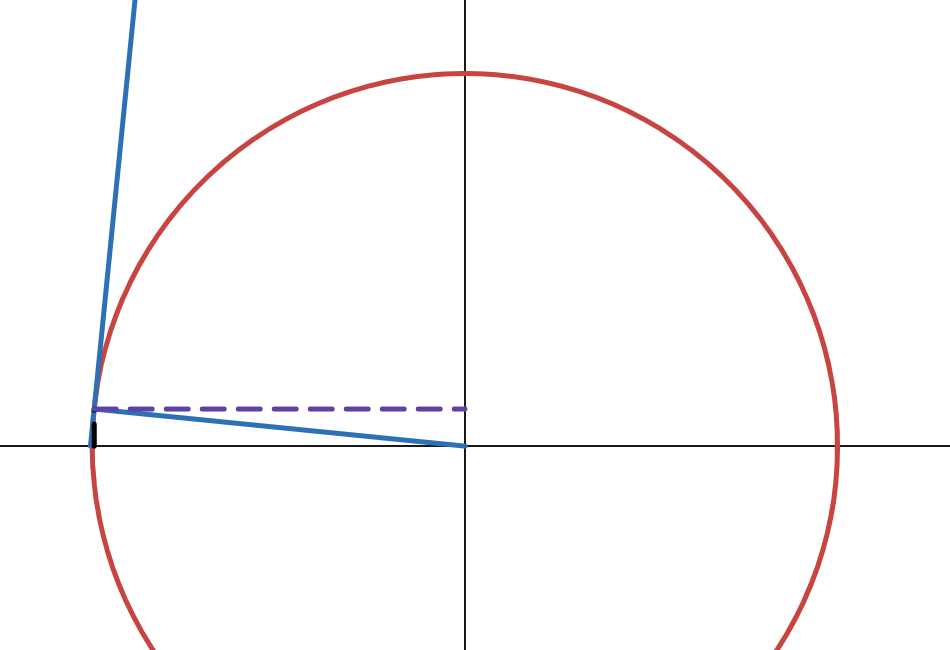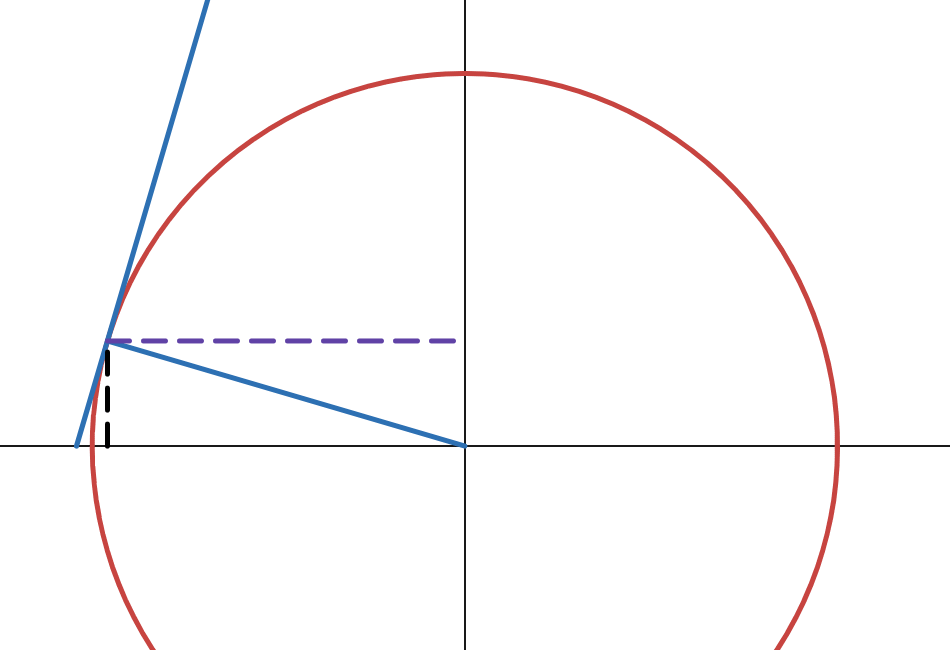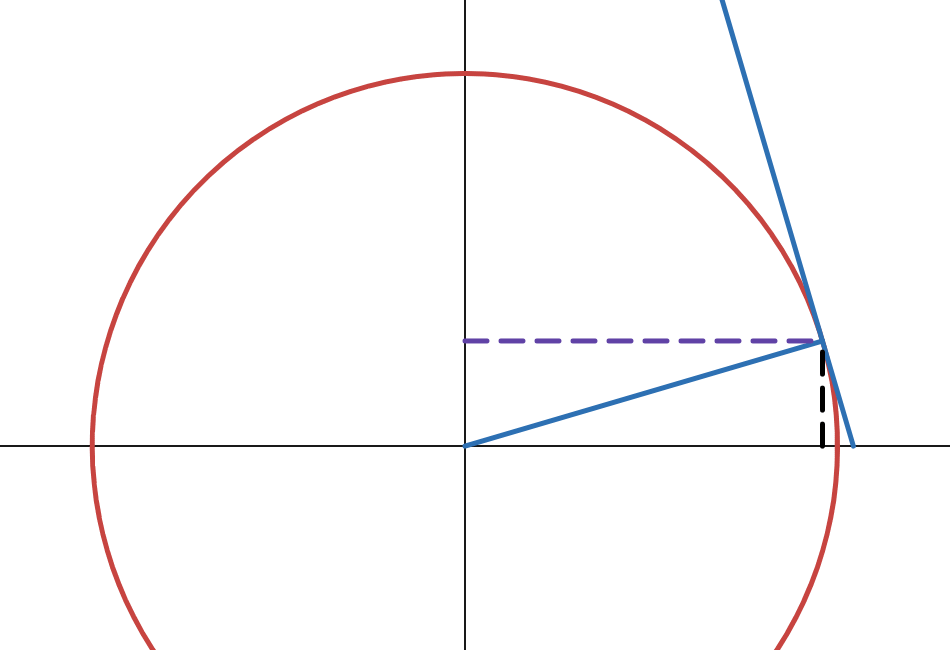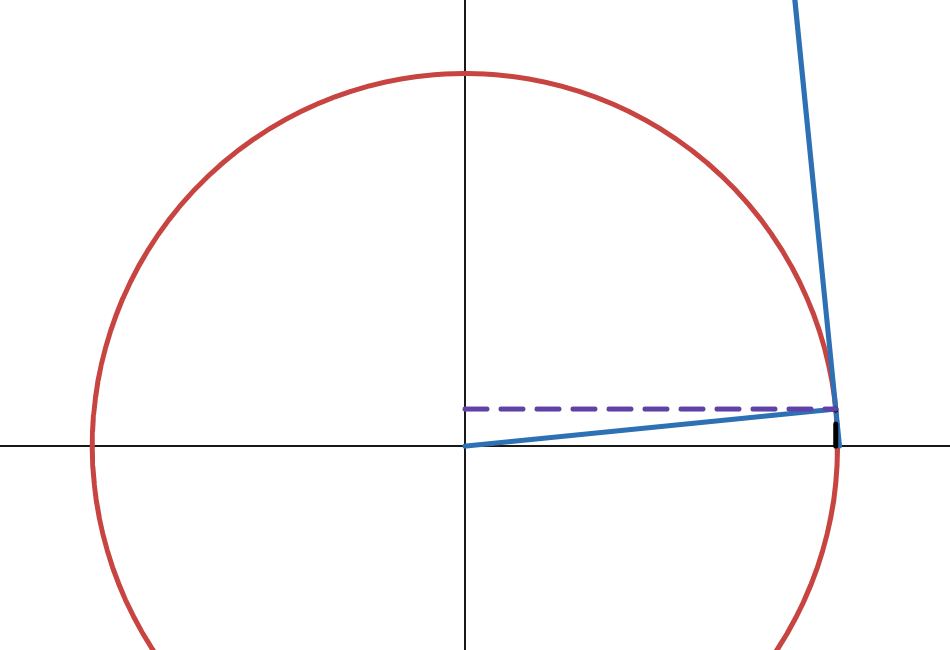
Let \(x\) be the length of the purple line, and \(\sqrt{1-x^2}\) be the length of the black line:
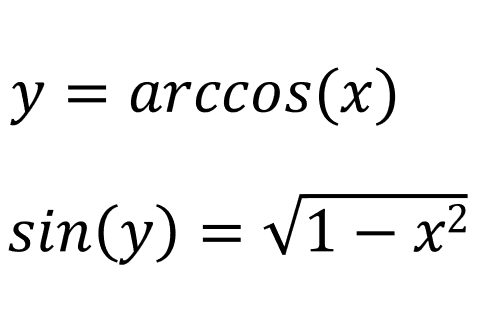
The range of \(\arccos(x)\) is \(y \in [0, \pi]\). Within this range, \(\sin(y)\) will always be positive. We already know that the derivative of x with respect to x is 1:

Since \(x = \cos(y)\):
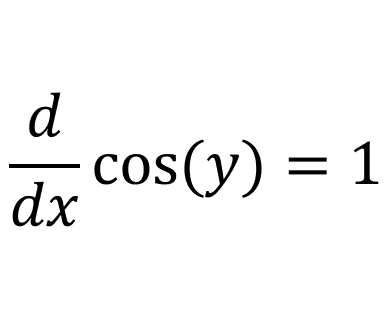
Using the chain rule:

And we already know what \(\sin(y)\) is equal to:
