Consider a series \(\sum_{n=1}^∞ a_n\). Let there be an integer \(N\) and a monotone decreasing function \(f\), such that \(f\) is defined on \([N, ∞)\) and \(f(n) = a_n\) for \(n \ge N\).
Suppose \(N=2\), and suppose \(f\) be monotone decreasing when \(x \gt 0\), then the left Riemann sum of \(\int^6_2 f(x) dx\) would be the sum of the rectangles shown below.
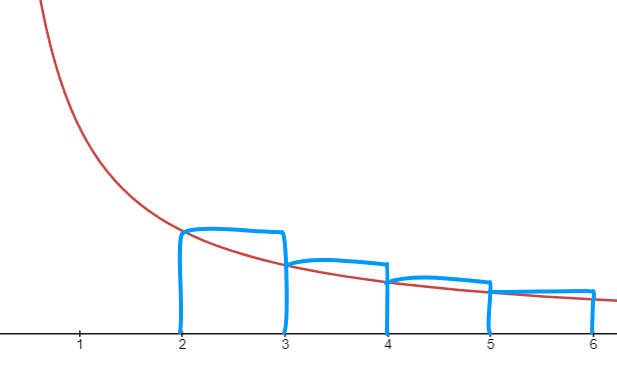
The area of the recantagle between 2 and 3 is \(f(2)*1 = a_2 *1 = a_2\), the area of the recantagle between 3 and 4 is \(f(3)*1 = a_3 *1 = a_3\), and so on.
\(\sum_{n=2}^5 a_n\) would be an overestimate of \(\int^6_2 f(x) dx\). This means:
The right Riemann sum of \(\int^5_2 f(x) dx\) would be the sum of the rectangles shown below:
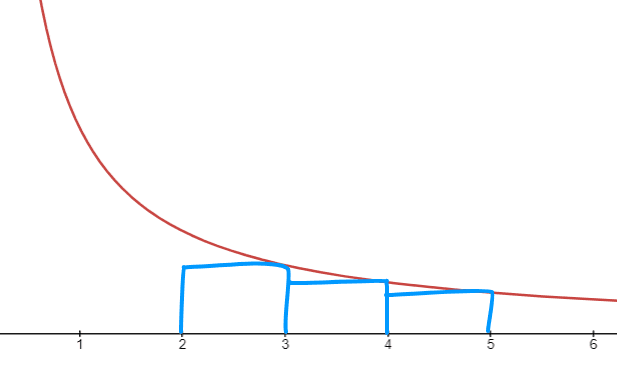
\(\sum_{n=3}^5 a_n\) would be an underestimate of \(\int^5_2 f(x) dx\). This means:
Putting them together:
We can generalize this:
If we take \(k \to \infty\):
If \(\int^\infty_N f(x) dx\) diverges, then so does \(\sum_{n=N}^\infty a_n\) because \(\int^\infty_N f(x) dx \le \sum_{n=N}^\infty a_n\) If \(\int^\infty_N f(x) dx\) converges, then so does \(\sum_{n=N}^\infty a_n\), because \(\sum_{n=N}^\infty a_n \le a_N + \int^\infty_N f(x) dx\). The contrapositive of these would also be true.