Any series whose terms alternate between positive and negative values is called an alternating series:
Where \(b_n \gt 0\). If \(0 \lt b_{n+1} \le b_n\) for all \(n\) and if \(\lim_{n \to \infty} b_n = 0\), then the series converges. This is known as the alternating series test. Let's try to understand why that's true.
Let \(S\) be the value of the infinite series (if it exists), and let \(S_k\) be the \(k\)th partial sum:
If \(0 \lt b_{n+1} \le b_n\) for all \(n\), then \(S_k\) for all \(k \ge 1\) will always be below or equal to \(b_1\).
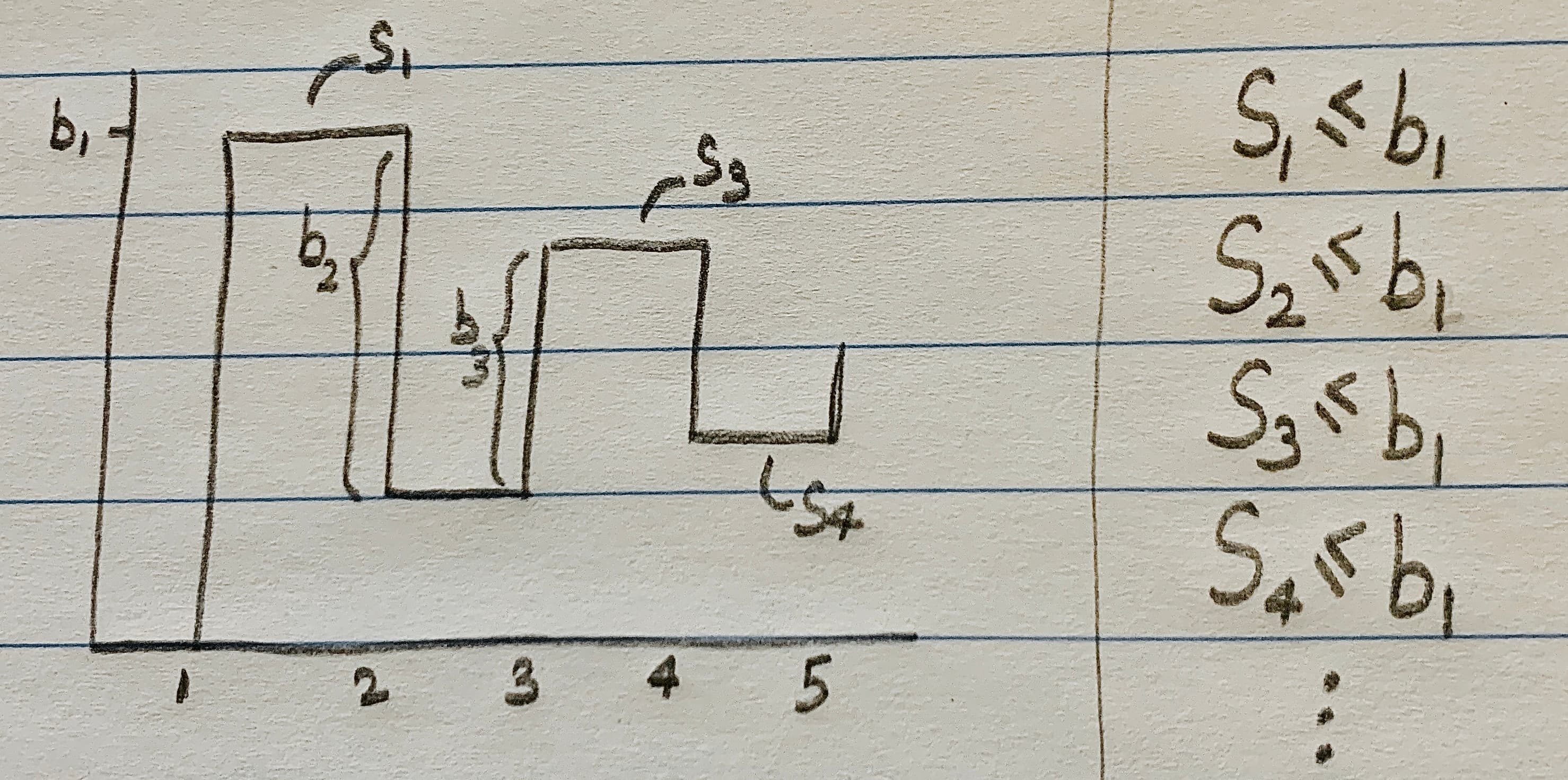
If \(b_{2n} \ge b_{2n+1}\), then \(b_{2n+1} - b_{2n}\) is some negative number. Therefore:
This means the sequence \(\{ S_{2k} \}\) would be an increasing sequence. Since \(\{S_{2k} \}\) will always be below or equal to \(b_1\), then \(\{S_{2k}\}\) would also be a bounded sequence, and by the monotone convergence theorem, it converges to some real number, let's call it \(L\):
Since \( S_{2k+1} = S_{2k} + b_{2k+1} \):
If \(\lim_{n \to \infty} b_n = 0\), then \(\lim_{k \to \infty} b_{2k+1} = 0\). Therefore:
This shows that both the odd and even partial sums are converges to \(L\). Since the infinite series \(S\) will always be less than the odd partials sums and more than the even partial sums, then, by the squeeze theorem, \(\lim_{n \to \infty} S_n = L\).