Lets say we have these two limits:
This means:
Before launching into the actual proof, let's do a little Algebra. First, expand the following product:
This gives us a new way of defining f(x)g(x), we will use that here:
Since "limx->af(x)-L = 0" and "limx->ag(x)-M = 0", then "limx->a[f(x)-L][g(x)-M] = 0" (the proof of this will be shown later). We can replace "limx->a[f(x)-L][g(x)-M]" with 0:
This means:
Our proof works if limx->a[f(x)-L][g(x)-M] = 0 is true, now lets try to proof this. For every number ε > 0, there is a number δ1 > 0 and a number δ2 > 0 such that:
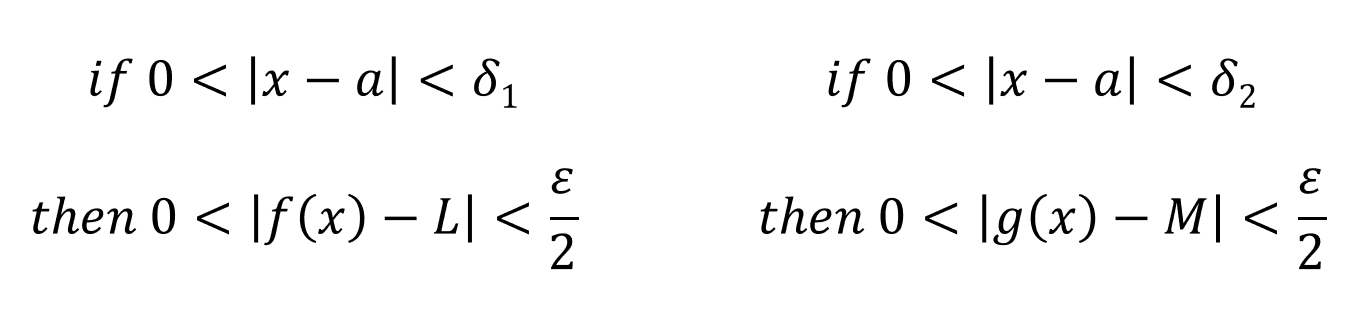
Let δ = min{δ1, δ2}:
This would mean limx->a[f(x)-L][g(x)-M] = 0.