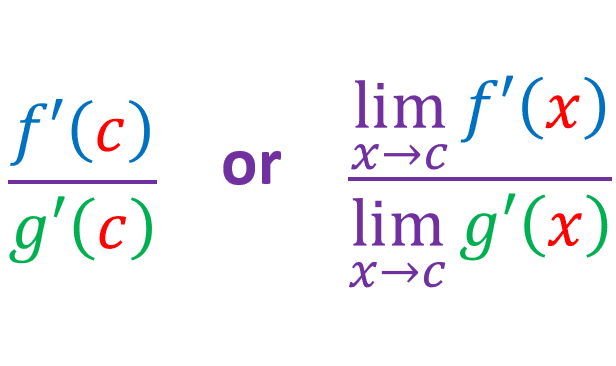Lets say there is a number c such that:
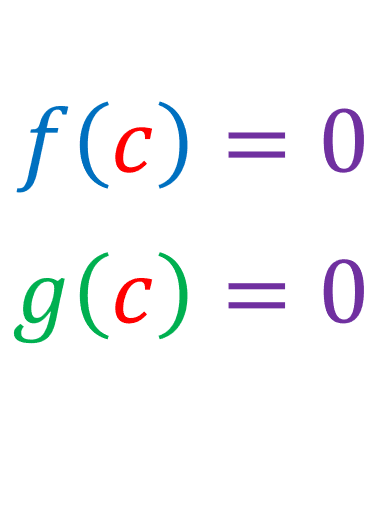
What we need to try to find is the limit of f(x)/g(x) as x approaches 0:
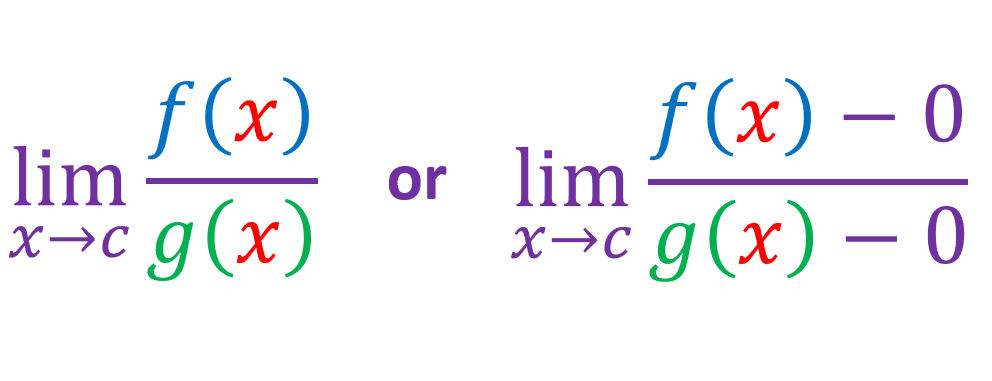
Since 0 = f(c) = g(c):
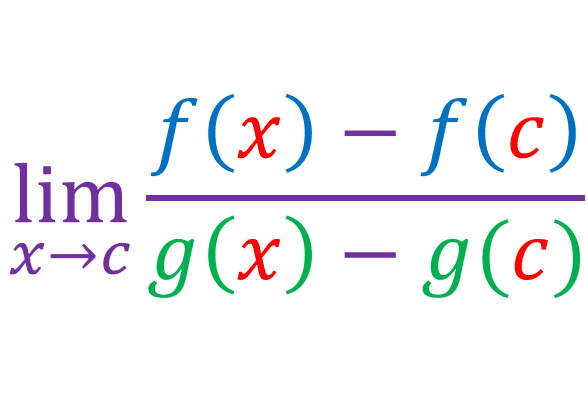
Which can be written as:

By using the limit laws:
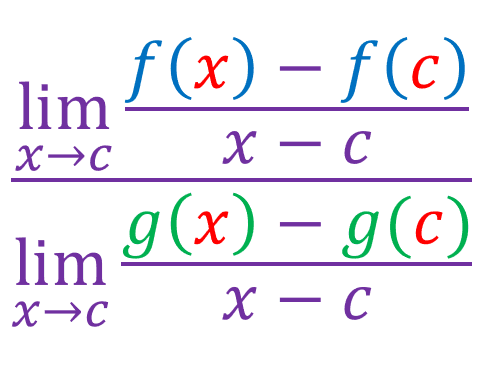
By definition of a derivative:
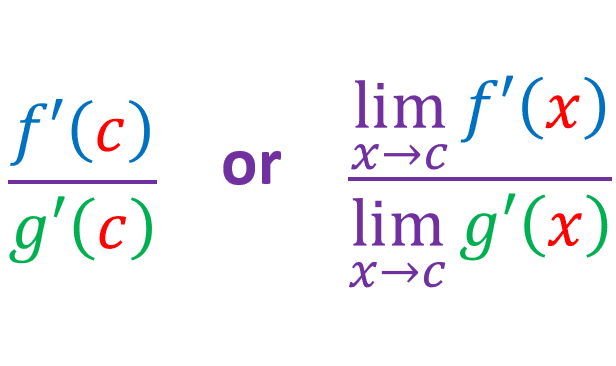
Lets say there is a number c such that:
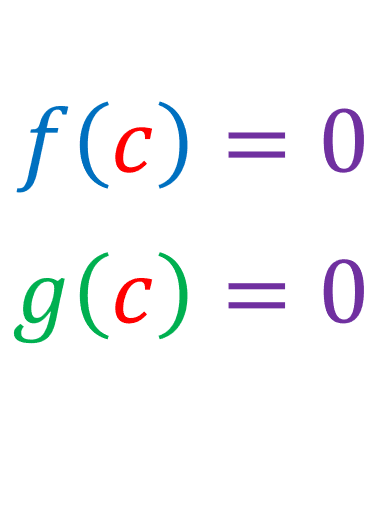
What we need to try to find is the limit of f(x)/g(x) as x approaches 0:
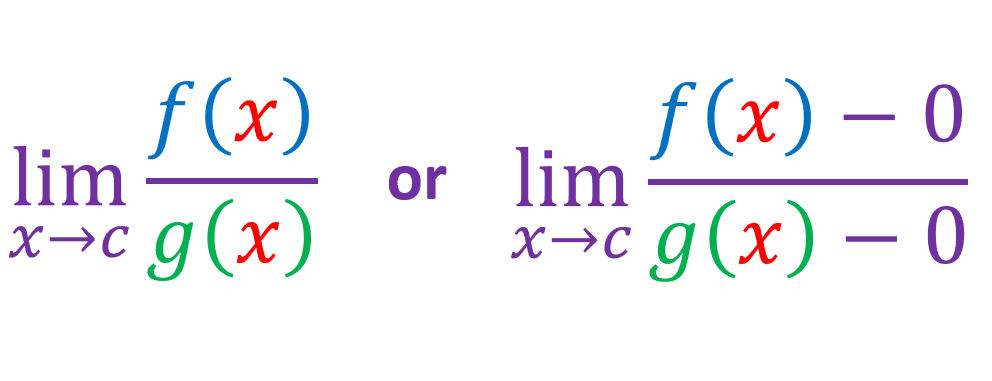
Since 0 = f(c) = g(c):
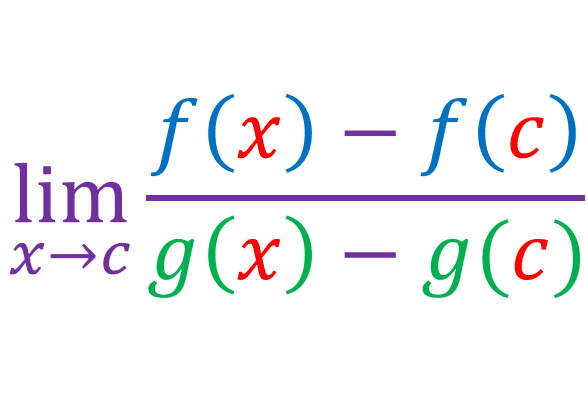
Which can be written as:

By using the limit laws:
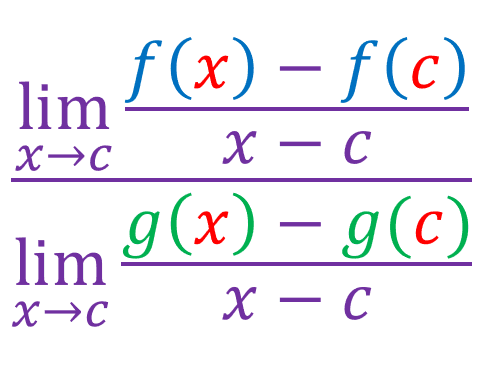
By definition of a derivative: