Consider the solid \(S\) extending along the x-axis:
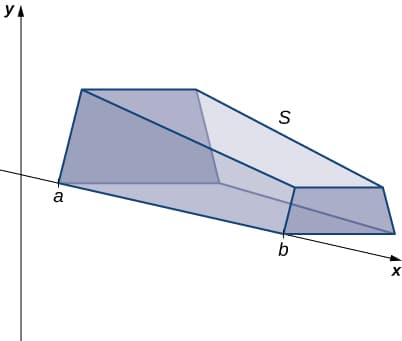
To find the volume of this solid, we will start by dividing \(S\) into slices perpendicular to the x-axis and finding the cross sectional area of those slices:

Let \(S_i\) represent the slice of \(S\) stretching from \(x_{i-1}\) to \(x_i\). For \(i=1,2, …, n\), let \(x^*_i\) be an arbitrary point in \([x_{i-1},x_i]\). Then the volume of slice \(S_i\)can be estimated by \(V(S_i)≈A(x^*_i)Δx\). The approximate volume will be more accurate if \(n\) is large.
Adding these approximations together, we see the volume of the entire solid \(S\) can be approximated by:
\[V(S)≈ \sum^n_{i=1} A(x^*_i)Δx\]
Our next step is to take the limit as \(n→∞\):
\[V(S)≈ \lim_{n \to \infty} \sum^n_{i=1} A(x^*_i)Δx = \int^b_a A(x) \ dx \]