Proof For The Fundamental Thoerem Of Calculus, Part 2

The second fundamental theorem of calculus states that if f is continuous on [a, b], then:

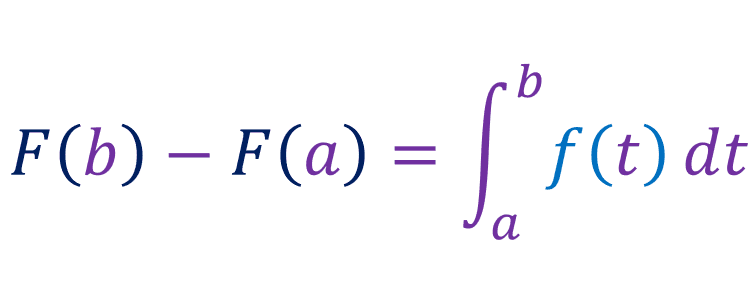
where F(x) is the antiderivative of f . Lets say the function f is continous on [a, b], and lets say function g is defined by:

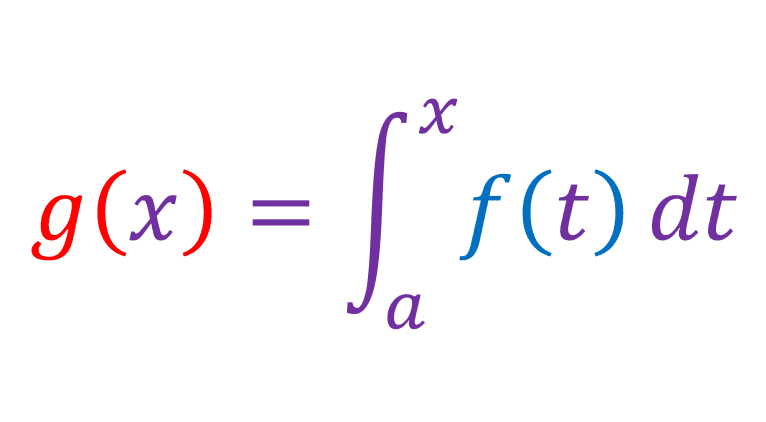
The variable x varies between a and b. Since g'(x) = f(x) . We can say that g(x) is the antiderivative of f(x) . The antiderivative of a function has an arbitrary constant. For example, the antiderivative of [x 2] is [(x 3 /3) + C], where C is an arbitrary constant. This is not the case with g(x), since you can find the value of C by using g(a) = 0. For example if f(x) = [x 2], and if a = 6, then g(6) = [(6 3 /3) + C], this means that [C = -72].

F(x) is like g(x), but where the arbitrary constant is unknown, so:

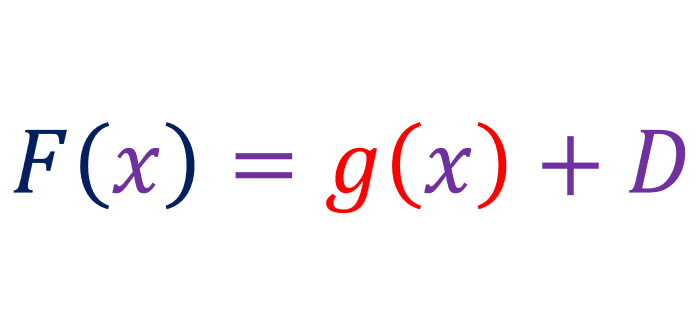
Where D is unknown. Now lets evaluate F(b) - F(a) :

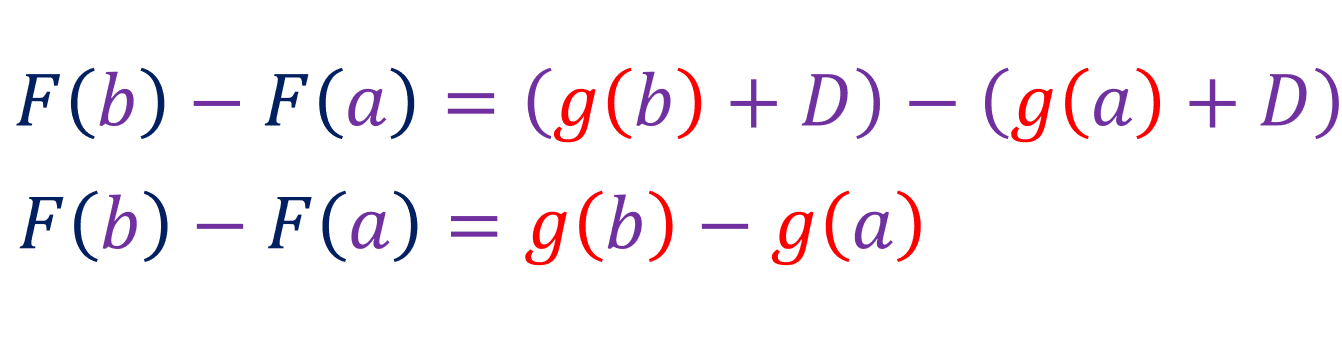
If we expand g :

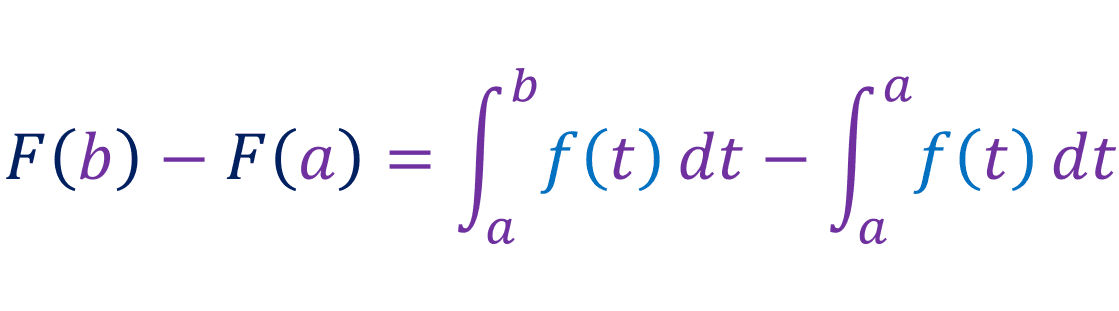
Since g(a) = 0:

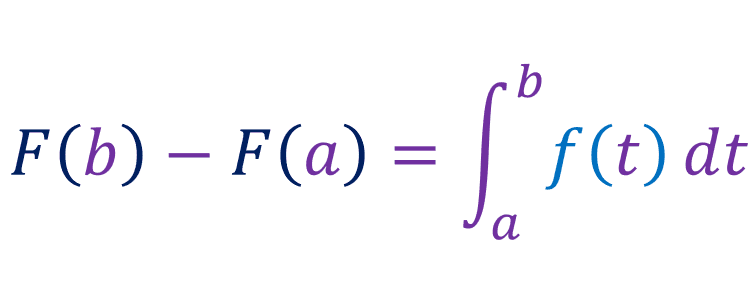
This is the fundamental theorem of calculus, part 2.

The above proof assumes that f is continuous on the whole interval [a, b]. The proof below will assume that \(f\) is Riemann integrable on the interval \([a, b]\). Let \(F\) be an antiderivative \(f\) on \((a, b)\) such that \(F\) is continuous on \([a, b]\). Let there be numbers \(x_0, \ldots, x_n\) such that:

\[a = x_0 < x_1 < \ldots < x_{n-1} < x_n = b\]

It follows that:

\[\begin{align} F(b) - F(a) &= F(x_n) - F(x_0) \\ &= F(x_n) - F(x_{n-1}) + F(x_{n-1}) - F(x_{n-2}) + F(x_{n-2}) - F(x_{n-3}) + \ldots + F(x_2) - F(x_1) + F(x_1) - F(x_0) \end{align}\]

We can rewrite this as:

\[F(b) - F(a) = \sum_{i=1}^n F(x_i) - F(x_{i-1})\]

According to the mean value theorem, for each \(i\) there exists a \(c_i\) in \((x_{i-1}, x_i)\) such that:

\[ \sum_{i=1}^n F(x_i) - F(x_{i-1}) = F'(c_i)(x_i - x_{i-1})\]

Therefore:

\[\begin{align} F(b) - F(a) &= \sum_{i=1}^n F'(c_i)(x_i - x_{i-1}) \\ &= \sum_{i=1}^n f(c_i)(\Delta x_i) \end{align}\]

We are describing the area of a rectangle, with the width times the height, and we are adding the areas together. As the size of the partitions get smaller and n increases, resulting in more partitions to cover the space, we get closer and closer to the actual area of the curve.

\[\lim_{\Delta x_i \to 0} F(b) - F(a) = \lim_{\Delta x_i \to 0} \sum_{i=1}^n f(c_i)(\Delta x_i) \]

Neither F(b) nor F(a) is dependent on \(\Delta x_i\):

\[F(b) - F(a) = \lim_{\Delta x_i \to 0} \sum_{i=1}^n f(c_i)(\Delta x_i) \]

The expression on the right side of the equation defines the integral over \(f\) from \(a\) to \(b\):

\[F(b) - F(a) = \int_a^b f(x) dx \]