Proof For The Fundamental Thoerem Of Calculus, Part 1

Lets say the function \(f(x)\) is continous on [a,b], and lets say function the \(F(x)\) is defined by:

\[ F(x) = \int^x_a f(t) \ dt \]

The function \(F(x)\) represents the area under the curve of \(f(x)\) from \(a\) to \(x\), where \(x\) varies between \(a\) and \(b\):

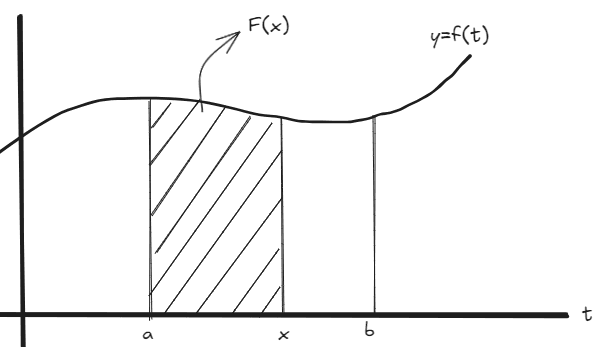
By definition of a derivative:

\[ F'(x) = \lim_{h \to 0} \frac{F(x+h)-F(x)}{h} \]

If we expand \(F(x)\):

\[ F'(x) = \lim_{h \to 0} \frac{ \int^{x+h}_a f(t) \ dt - \int^{x}_a f(t) \ dt }{h} \]

We can rewrite this as:

\[ \begin{align} F'(x) &= \lim_{h \to 0} \frac{ \int^{x}_a f(t) \ dt + \int^{x+h}_x f(t) \ dt - \int^{x}_a f(t) \ dt }{h} \\ &= \lim_{h \to 0} \frac{ \int^{x+h}_x f(t) \ dt }{h} = \lim_{h \to 0} \frac{1}{h} \left( \int^{x+h}_x f(t) \ dt \right) \end{align}\]

Before going any further, let's first think about just integral of \( f(t)\) between \(x\) and \(x+h\):

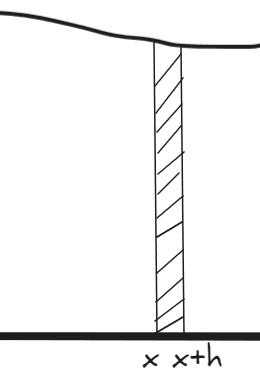
This area can be represented in two ways, one is the integral, and the second is the average value of \(f\) in [x, x+h] times the interval width (\(h\)):

\[A = \int^{x+h}_x f(t) \ dt = f_{avg}(t) * (h) \]

This means:

\[ f_{avg}(t) = \frac{1}{h} \int^{x+h}_x f(t) \ dt \]

Going back to \(F'(x)\):

\[ F'(x) = \lim_{h \to 0} \frac{1}{h} \int^{x+h}_x f(t) = \lim_{h \to 0} f_{avg}(t) \]

where \(f_{avg}(t)\) is the average value of \(f\) in [x, x+h]. This means if \(h \to 0\), then \(f_{avg}(t) = f(x)\), so:

\[ F'(x) = f(x) \]

This is the fundamental theorem of calculus (part 1).

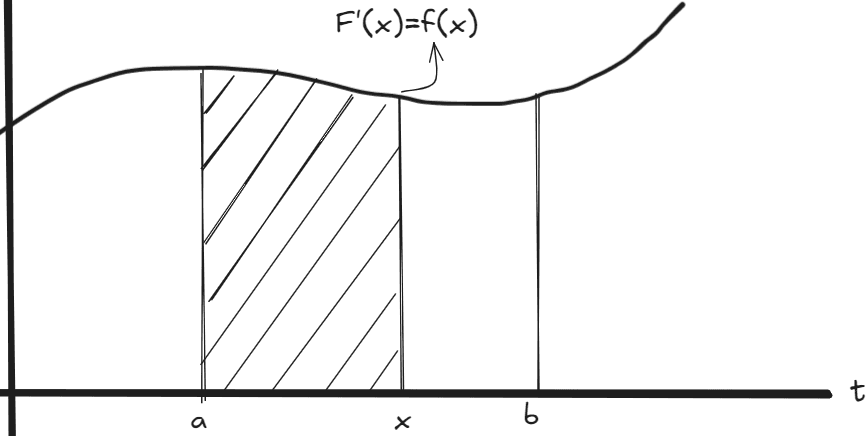
\(F'(x) = f(x)\) means a tiny increase of \(F(x)\) at \(x\) is equal to \(f(x)\). Also, the lower bound of the integral (\(a\)) has no affect on \(F'(x)\).