Let \(f(x)\) be a smooth function defined over \([a,b]\). We want to calculate the length of the curve from the point \((a,f(a))\) to the point \((b,f(b))\). If we want to find the area under the curve, we would divide the area into \(n\) rectangles and add the area of those rectangles:
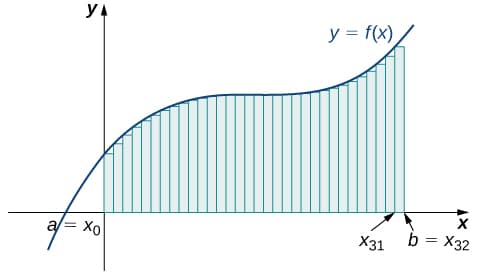
The estimate of the area under the curve would get better and better as \(n \to \infty\). Can we do a similar thing with the arc length (i.e. divide the arc into \(n\) horizontal intervals and add the width of those intervals)? The problem with this is that for any curve, the estimated length will always be \(\lim_{n \to \infty} \Delta x = \int_a^b dx = b-a\). This is clearly wrong. Instead, for \(i=1,2,…,n\), we can construct a line segment from the point \((x_{i-1},f(x_{i-1}))\) to the point \((x_i,f(x_i))\):
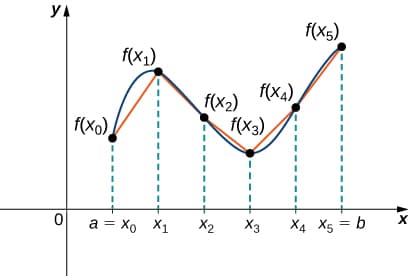
To find the length of each line segment, we look at the change in vertical distance as well as the change in horizontal distance over each interval:
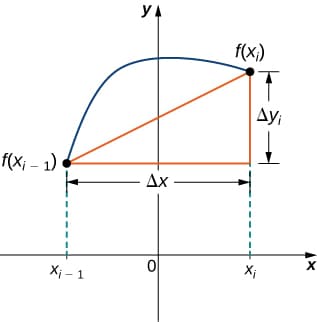
By the Pythagorean theorem the length of the line segment \(s\) is:
According to the Mean Value Theorem, there should be a value \(x_i^*\) such that \(f'(x_i^*) = \frac{\Delta y_i}{\Delta x}\).:
Adding up all the segments we get:
Taking the limit as \(n→∞\):