Let [h(x) = f(x)*g(x)]. By definition of a derivative, the derivative of h(x) is:
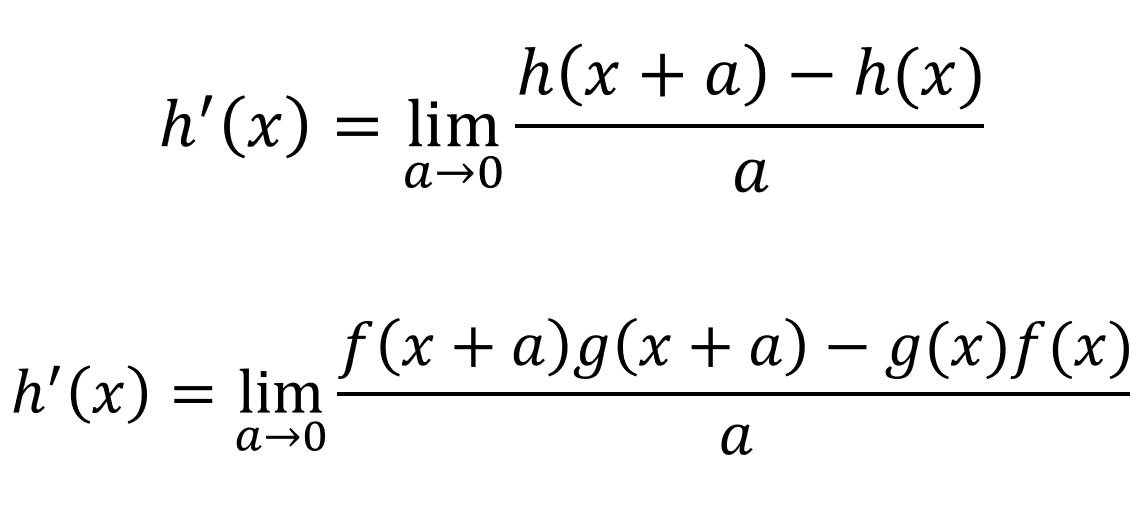
Since [-f(x)*g(x+a) + f(x)*g(x+a) = 0]:

Now we split the fraction:

If we use the limit laws:
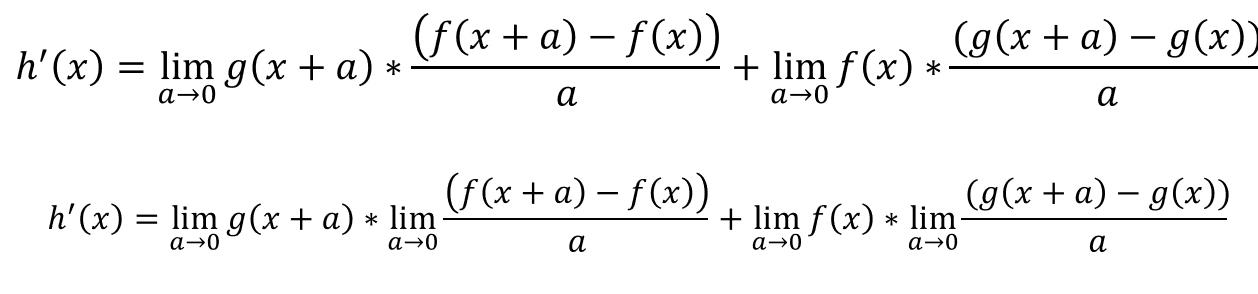
If we simplify:

And that completes our proof.
Let [h(x) = f(x)*g(x)]. By definition of a derivative, the derivative of h(x) is:
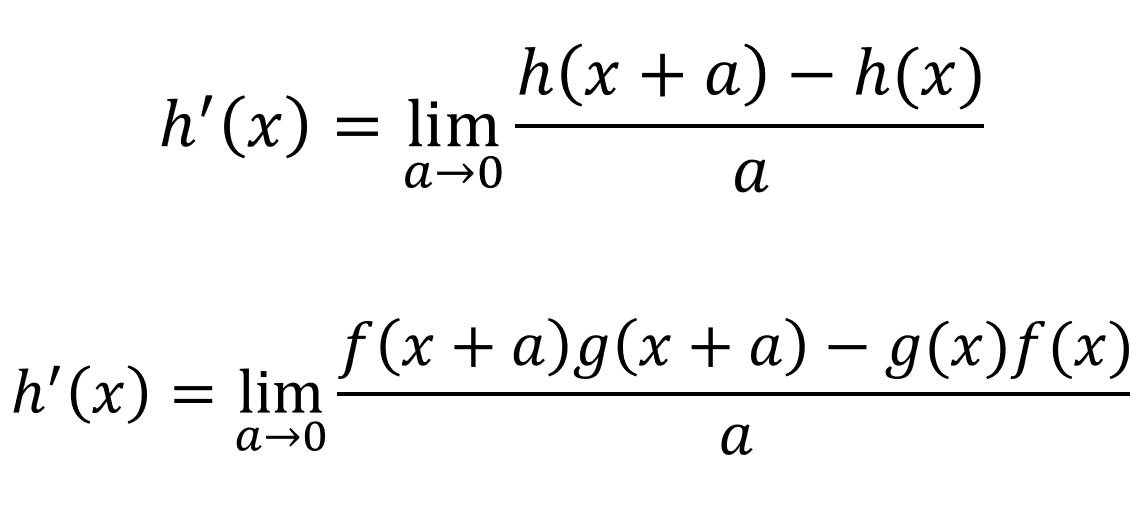
Since [-f(x)*g(x+a) + f(x)*g(x+a) = 0]:

Now we split the fraction:

If we use the limit laws:
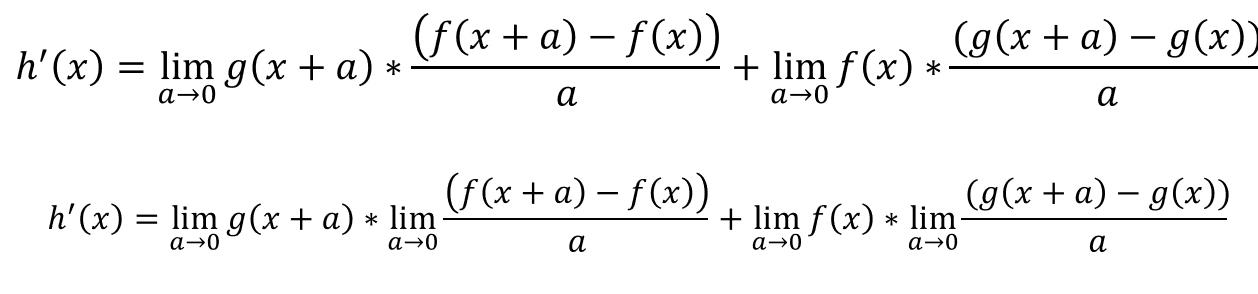
If we simplify:

And that completes our proof.