The Mean Value Theorem states that if function \(f\) is continuous over the closed interval \([a,b]\) and differentiable over the open interval \((a,b)\). Then, there exists at least one point \(c∈(a,b)\) such that:
\[f'(c) = \frac{f(b)-f(a)}{b-a} \]
Consider the line connecting \((a,f(a))\) and \((b,f(b))\). The gradient of this line is:
\[\frac{f(b)-f(a)}{b-a} \]
The equation of this line is:
\[y = \frac{f(b)-f(a)}{b-a} (x-a) + f(a)\]
Let \(g(x)\) be the vertical difference between the point \((x,f(x))\) and the point \((x,y)\) on that line:
\[g(x) = f(x) - \left[ \frac{f(b)-f(a)}{b-a} (x-a) + f(a) \right]\]
Example:
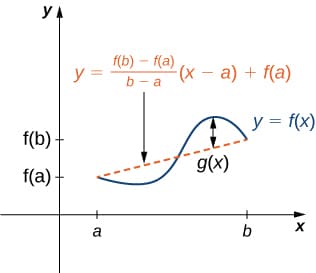
Since the two lines intersect at \(x=a\) and \(x=b\), then \(g(a) = 0 = g(b)\). According to Rolle's Theorem, there should be a point \(c\) between \(a\) and \(b\) where \(g'(c)=0\). The derivative of \(g'(x)\) is:
\[g'(x) = f'(x) - \frac{f(b)-f(a)}{b-a}\]
At \(c\), this would be:
\[0 = f'(c) - \frac{f(b)-f(a)}{b-a}\]
So:
\[f'(c) = \frac{f(b)-f(a)}{b-a}\]